Welcome to Shanshan Blog!
-
Machine Learning Logistic Regression
Why Logistic Regression?
Simple logistic regression is analogous to linear regression, except that the dependent variable is nominal, not a measurement. One goal is to see whether the probability of getting a particular value of the nominal variable is associated with the measurement variable; the other goal is to predict the probability of getting a particular value of the nominal variable, given the measurement variable.
The Binomial Distribution
We consider first the case where the response yi is binary, assuming only two values that for convenience we code as one or zero. For example, we could define
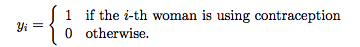
How Does Logistic Regression Work?
Step 1: To Find hypothesis function
We use Sigmoid Function in this algorithm:
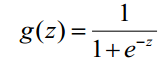
It has beautiful “S” shape:
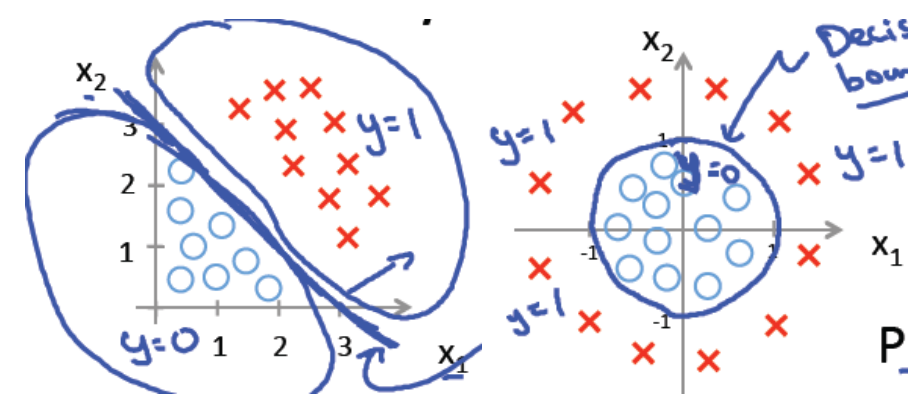
The left one is linear decision border, The right one is non-linear decision border:
For linear decision border, the formula is:
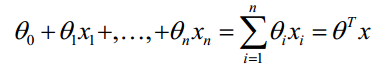
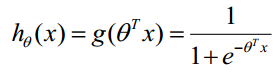
Function h(X) has special meaning, it means the probability of the result is 1,
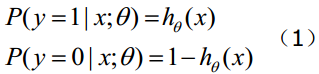
Step 2: To create Cost Function and J Function
It is calculated based on maximum likelihood method
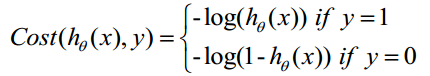
Step 3: To get minimum J function and get the parameter theta
Use Gradient Descent:
Update theta
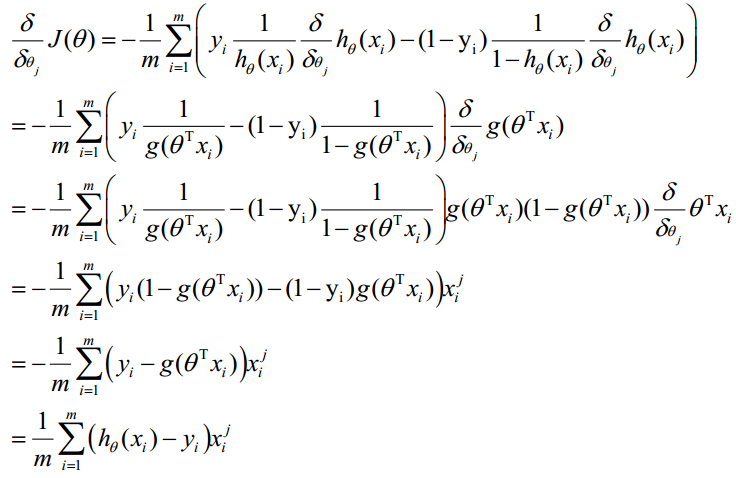
So it is:
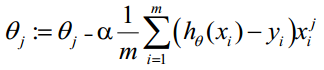
-
Google APAC 2017 University Test Round D Problem B Sitting
Problem
The Codejamon game is on fire! Many players have gathered in an auditorium to fight for the World Championship. At the opening ceremony, players will sit in a grid of seats with R rows and C columns.
The competition will be intense, and the players are sensitive about sitting near too many of their future opponents! A player will feel too crowded if another player is seated directly to their left and another player is seated directly to their right. Also, a player will feel too crowded if one player is seated directly in front of them and another player is seated directly behind them.
What is the maximum number of players that can be seated such that no player feels too crowded?
Input and Output
Input
The first line of the input gives the number of test cases, T. T test cases follow. Each test case consists of one line with two integers R and C: the number of rows and columns of chairs in the auditorium.
Output
For each test case, output one line containing Case #x: y, where x is the test case number (starting from 1) and y is the maximum number of players that can be seated, as described in the problem statement.
Limits
1 ≤ T ≤ 100.
Small dataset
1 ≤ R ≤ 5.
1 ≤ C ≤ 5.
Large dataset
1 ≤ R ≤ 100.
1 ≤ C ≤ 100.
Sample
Input 3 2 2 2 3 4 1 Output Case #1: 4 Case #2: 4 Case #3: 3In sample case #1, we can fill all seats, and no player will feel too crowded.
In sample case #2, each row has three seats. We can’t put three players in a row, since that would make the middle player feel too crowded. One optimal solution is to fill each of the first two columns, for a total of four players.
In sample case #3, one optimal solution is to fill the first two rows and the last row, for a total of three players.
The idea is from http://blog.csdn.net/dumeichen/article/details/52916711
Codes
#include <iostream> #include <algorithm> using namespace std; /* for one row, the maximum numbers are m - m/3 for three rows, the maximum numbers are 2*m for n (n>3) rows, the first row has to be k = m-m/3 n/3 use 2*m the ways to fill in n%3 if there still is one row, fill in m-m/3 if there still are two rows, the rules are: consider the relationship between m%3 and the numbers of every row 1. the first row has to be k = m-m/3 2. when m%3==0, three rows numbers must be k, k, k when m%3==1, three rows numbers must be k, k, k-1 when m%3==2, three rows numbers must be k, k-1, k-1 so if m%3!= 2, the two rows both must be filled in k and k, otherwise it should be k and k-1 */ int main() { freopen("//Downloads//B-small-practice.in","r",stdin); freopen("//Downloads//B-small-attempt0.out","w",stdout); int num; cin >> num; int m, n; for (int i=0; i<num; i++) { cin >> n >> m; int res=0; if (n>m) swap(n, m); int k = m - m/3; // the maximum numbers in one row res += n/3 * 2 * m; int temp = n%3; if (temp==1) res += k; else if (temp==2) { if (m%3==2 && n>3) res = res+(k+k-1); else res = res+2*k; } cout << "Case #" << i+1 << ": " << res << endl; } return 0; }
-
Google APAC 2017 University Test Round D Problem A Partioning Number
Problem
A and B are the only two candidates competing in a certain election. We know from polls that exactly N voters support A, and exactly M voters support B. We also know that N is greater than M, so A will win.
Voters will show up at the polling place one at a time, in an order chosen uniformly at random from all possible (N + M)! orders. After each voter casts their vote, the polling place worker will update the results and note which candidate (if any) is winning so far. (If the votes are tied, neither candidate is considered to be winning.)
What is the probability that A stays in the lead the entire time – that is, that A will always be winning after every vote?
Input and Output
Input
The input starts with one line containing one integer T, which is the number of test cases. Each test case consists of one line with two integers N and M: the numbers of voters supporting A and B, respectively.
Output
For each test case, output one line containing Case #x: y, where x is the test case number (starting from 1) and y is the probability that A will always be winning after every vote.
y will be considered correct if y is within an absolute or relative error of 10-6 of the correct answer. See the FAQ for an explanation of what that means, and what formats of real numbers we accept.
Limits
1 ≤ T ≤ 100.
Small dataset
0 ≤ M < N ≤ 10.
Large dataset
0 ≤ M < N ≤ 2000.
Sample
Input 2 2 1 1 0 Output Case #1: 0.33333333 Case #2: 1.00000000In sample case #1, there are 3 voters. Two of them support A – we will call them A1 and A2 – and one of them supports B. They can come to vote in six possible orders: A1 A2 B, A2 A1 B, A1 B A2, A2 B A1, B A1 A2, B A2 A1. Only the first two of those orders guarantee that Candidate A is winning after every vote. (For example, if the order is A1 B A2, then Candidate A is winning after the first vote but tied after the second vote.) So the answer is 2/6 = 0.333333…
In sample case #2, there is only 1 voter, and that voter supports A. There is only one possible order of arrival, and A will be winning after the one and only vote.

Codes
#include <iostream> using namespace std; /* 扩展卡特兰数 n个1,m个0,n > m 要保证任意一个位置1的个数都大于0的个数。 保证第一个数为1,后面n - 1个1和m个0符合扩展卡特兰数即可 n - 1个1,m个0构成的卡特兰数的最终解为ans = C(n + m - 1, n - 1) - C(n + m - 1,n) */ int main() { freopen("//Downloads//A-large-practice.in","r",stdin); freopen("//Downloads//A-large-attempt0.out","w",stdout); int num; cin >> num; int M, N; for (int i=0; i<num; i++) { cin >> N >> M; double ans = (N-M) * 1.0 / (N+M); cout << "Case #" << i+1 << ": " << ans << endl; } return 0; }
-
Google APAC 2017 University Test Round E Problem C Partioning Number
Problem
Shekhu has N balls. She wants to distribute them among one or more buckets in a way that satisfies all of these constraints:
The numbers of balls in the buckets must be in non-decreasing order when read from left to right.
The leftmost bucket must be non-empty and the number of balls in the leftmost bucket must be divisible by D.
The difference (in number of balls) between any two buckets (not just any two adjacent buckets) must be less than or equal to 2.
How many different ways are there for Shekhu to do this? Two ways are considered different if the lists of numbers of balls in buckets, reading left to right, are different.
Input and Output
Input
The first line of the input gives the number of test cases, T. T test cases follow. Each test case consists of one line with two integers N and D, as described above.
Output
For each test case, output one line containing Case #x: y, where x is the test case number (starting from 1) and y is the answer, as described above.
Limits
1 ≤ T ≤ 100.
1 ≤ D ≤ 100.
Small dataset
1 ≤ N ≤ 2000.
Large dataset
1 ≤ N ≤ 100000.
Sample
Input 3 7 1 7 2 2 4 Output Case #1: 10 Case #2: 1 Case #3: 0 In sample case #1, the possible distributions are: 1 1 1 1 1 1 1 1 1 1 1 1 2 1 1 1 1 3 1 1 1 2 2 1 2 2 2 1 1 2 3 1 3 3 2 2 3 3 4 7Note that 1 2 4 is not a valid distribution, since the difference between 1 and 4 is more than 2.
In sample case #2, the possible distributions are:
2 2 3
3 4 is not possible, since the first term is not divisible by 2.
In sample case #3, no possible arrangement exists.
Codes
#include <iostream> using namespace std; long long getPartioning(int num, int d) { long long res = 0; int i,k,m,l,r; for (i=d; i<num; i+=d) for (k=(num-1-i)/(i+2)+2; k<=num/i; k++) { m = num-k*i; l = m-k+1; if (l<0) l=0; r = m/2; if (r>k-1) r=k-1; if (l<=r) res+=(r-l+1); } if (num%d ==0) res++; return res; } int main() { freopen("//Downloads//C-small-practice.in","r",stdin); freopen("//Downloads//C-small-attempt0.out","w",stdout); int N; cin >> N; int num, d; for (int i=0; i<N; i++) { cin >> num >> d; cout << "Case #" << i+1 << ": " << getPartioning(num, d) << endl; } return 0; }
-
Google APAC 2017 University Test Round E Problem B Beautiful Numbers
Problem
We consider a number to be beautiful if it consists only of the digit 1 repeated one or more times. Not all numbers are beautiful, but we can make any base 10 positive integer beautiful by writing it in another base.
Given an integer N, can you find a base B (with B > 1) to write it in such that all of its digits become 1? If there are multiple bases that satisfy this property, choose the one that maximizes the number of 1 digits.
Input and Output
Input
The first line of the input gives the number of test cases, T. T test cases follow. Each test case consists of one line with an integer N.
Output
For each test case, output one line containing Case #x: y, where x is the test case number (starting from 1) and y is the base described in the problem statement.
Limits
1 ≤ T ≤ 100.
Small dataset
3 ≤ N ≤ 1000.
Large dataset
3 ≤ N ≤ 1018.
Sample
Input 2 3 13 Output Case #1: 2 Case #2: 3In case #1, the optimal solution is to write 3 as 11 in base 2.
In case #2, the optimal solution is to write 13 as 111 in base 3. Note that we could also write 13 as 11 in base 12, but neither of those representations has as many 1s.
Codes
#include <iostream> #include <cmath> using namespace std; bool isvalid(long long num, long long j) { while (num) { if (num % j != 1) return false; num /= j; } return true; } int main() { freopen("//Downloads//B-large-practice.in","r",stdin); freopen("//Downloads//B-large-attempt0.out","w",stdout); int N; cin >> N; long long num; for (int i=0; i<N; i++) { cin >> num; // long long half = sqrt(num); for (long long j=2; j<=num; j++) { if (isvalid(num, j)) { cout << "Case #" << i+1 << ": " << j << endl; break; } } } return 0; }
-
Google APAC 2017 University Test Round E Problem A Diwali lightings
Problem
Diwali is the festival of lights. To celebrate it, people decorate their houses with multi-color lights and burst crackers. Everyone loves Diwali, and so does Pari. Pari is very fond of lights, and has transfinite powers, so she buys an infinite number of red and blue light bulbs. As a programmer, she also loves patterns, so she arranges her lights by infinitely repeating a given finite pattern S.
For example, if S is BBRB, the infinite sequence Pari builds would be BBRBBBRBBBRB…
Blue is Pari’s favorite color, so she wants to know the number of blue bulbs between the Ith bulb and Jth bulb, inclusive, in the infinite sequence she built (lights are numbered with consecutive integers starting from 1). In the sequence above, the indices would be numbered as follows:
B B R B B B R B B B R B... 1 2 3 4 5 6 7 8 9 10 11 12So, for example, there are 4 blue lights between the 4th and 8th positions, but only 2 between the 10th and 12th.
Since the sequence can be very long, she wrote a program to do the count for her. Can you do the same?
Input and Output
Input
The first line of the input gives the number of test cases, T. T test cases follow.
First line of each test case consists of a string S, denoting the initial finite pattern.
Second line of each test case consists of two space separated integers I and J, defined above.
Output
For each test case, output one line containing Case #x: y, where x is the test case number (starting from 1) and y is number of blue bulbs between the Ith bulb and Jth bulb of Pari’s infinite sequence, inclusive.
Limits
1 ≤ T ≤ 100.
1 ≤ length of S ≤ 100.
Each character of S is either uppercase B or uppercase R.
Small dataset
1 ≤ I ≤ J ≤ 106.
Large dataset
1 ≤ I ≤ J ≤ 1018.
Sample
Input 3 BBRB 4 8 BBRB 10 12 BR 1 1000000 Output Case #1: 4 Case #2: 2 Case #3: 500000Codes
#include <iostream> #include <fstream> #define LL long long using namespace std; void countF(string pattern, LL left, LL right) { int len = pattern.size(); LL l1 = left / len, l2 = left % len; LL r1 = right / len, r2 = right % len; LL count = 0, ll = 0, rr = 0; for (int i=0; i<len; i++) { if (pattern[i] == 'B') count++; if (i+1 == l2) ll = count; if (i+1 == r2) rr = count; } LL sum1 = r1*count+rr; LL sum2 = l1*count+ll; cout << sum1 - sum2 << endl; } int main() { int N; LL left, right; freopen("//Downloads//A-large-practice.in","r",stdin); freopen("//Downloads//A-large-attempt0.out","w",stdout); cin >> N; string pattern; for (int i=0; i<N; i++) { cin >> pattern; cin >> left >> right; printf("Case #%d: ",i+1); countF(pattern, left-1, right); } return 0; }