Welcome to Shanshan Blog!
-
Linear Regression Example in Python
import pandas as pd import seaborn as sns import matplotlib.pyplot as plt from sklearn.utils import check_array from sklearn.model_selection import train_test_split from sklearn.linear_model import LinearRegression from sklearn import metrics import numpy as np data = pd.read_csv('http://www-bcf.usc.edu/~gareth/ISL/Advertising.csv', index_col=0) print data.head() sns.pairplot(data, x_vars=['TV', 'Radio', 'Newspaper'], y_vars='Sales', size=7, aspect=0.8) plt.show() # from the figure, we can see there exits strong linear relationship between TV and sales, # 'reg' 95% sns.pairplot(data, x_vars=['TV','Radio','Newspaper'], y_vars='Sales', size=7, aspect=0.8, kind='reg') plt.show() # linear regression model feature_cols = ['TV', 'Radio', 'Newspaper'] x = data[feature_cols] # check the type and shape print type(x) print x.shape y = data['Sales'] print type(y) print y.shape # trainging and test data x_train, x_test, y_train, y_test = train_test_split(x, y, random_state=1) linreg = LinearRegression() linreg.fit(x_train, y_train) print linreg.intercept_ print linreg.coef_ print zip(feature_cols, linreg.coef_) y_pred = linreg.predict(x_test) # evaluate the model # calculate MAE using scikit-learn, Mean Absolute Error print "MAE using scikit-learn: ", metrics.mean_absolute_error(y_test, y_pred) # calculate MSE using scikit-learn, Mean Squared Error print "MSE using scikit-learn", metrics.mean_squared_error(y_test, y_pred) # calculate RMSE using scikit-learn, Root Mean Squared Error print "RMSE:",np.sqrt(metrics.mean_squared_error(y_test, y_pred)) # as we can see newspaper is weak-relationship with Sales, so remove the feature feature_cols = ['TV', 'Radio'] x = data[feature_cols] y = data.Sales x_train, x_test, y_train, y_test = train_test_split(x, y, random_state=1) linreg.fit(x_train, y_train) y_pred = linreg.predict(x_test) print np.sqrt(metrics.mean_squared_error(y_test, y_pred))Scatter Figure
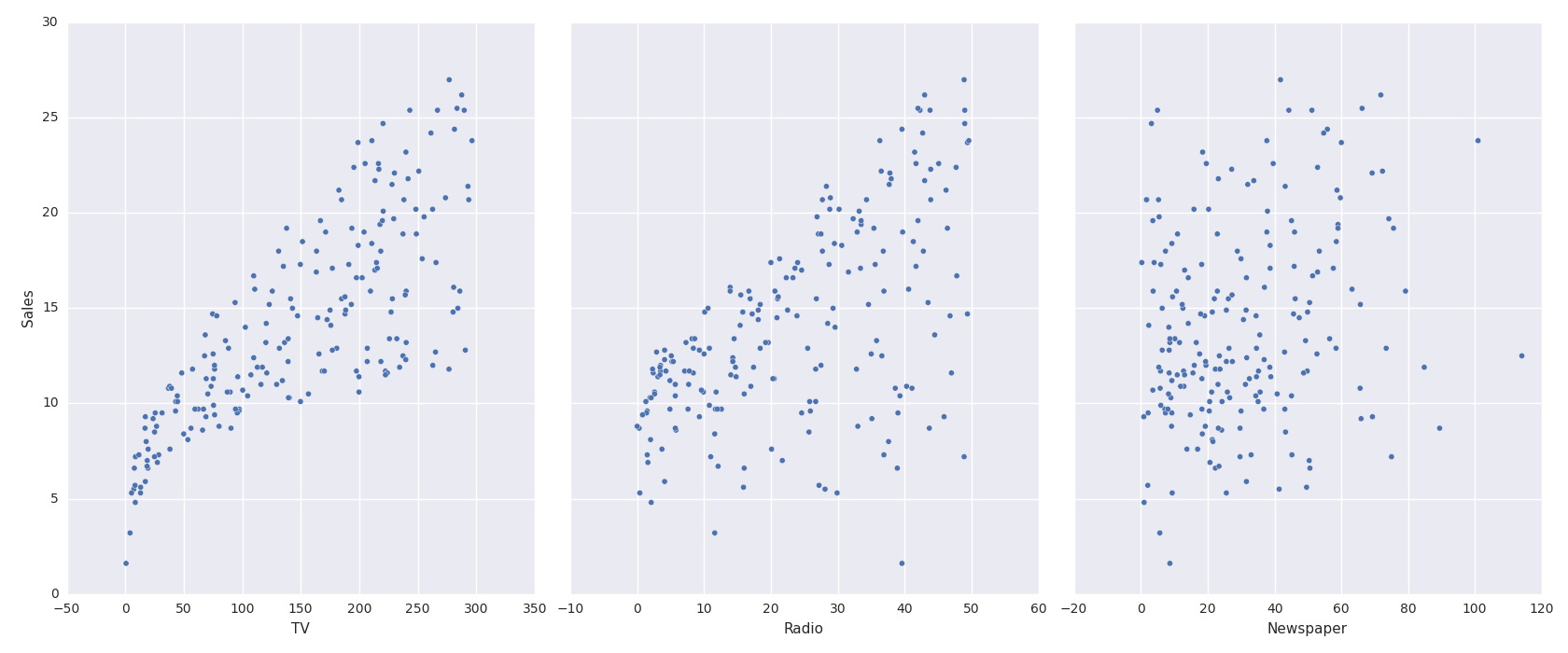Linear Regression Figure
-
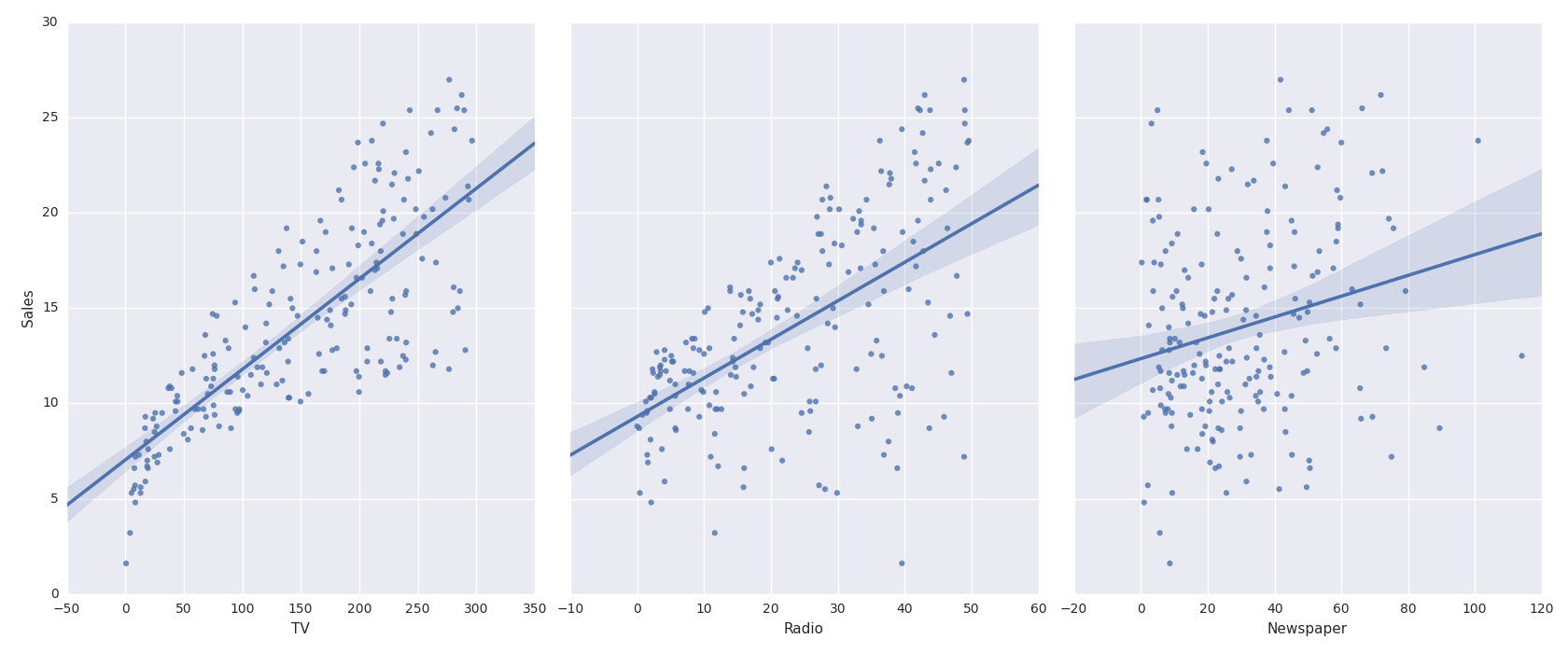
Leetcode (112, 113) Path Sum I, II
Leetcode 112. Path Sum
Given a binary tree and a sum, determine if the tree has a root-to-leaf path such that adding up all the values along the path equals the given sum.
class Solution { public: bool hasPathSum(TreeNode* root, int sum) { if (!root) return false; if (!root->left && !root->right && root->val == sum) return true; return hasPathSum(root->left, sum-root->val) || hasPathSum(root->right, sum-root->val); } };Leetcode 113. Path Sum II
Given a binary tree and a sum, find all root-to-leaf paths where each path’s sum equals the given sum.
For example: Given the below binary tree and sum = 22, 5 / \ 4 8 / / \ 11 13 4 / \ / \ 7 2 5 1 return [[5,4,11,2],[5,8,4,5]]class Solution { public: vector<vector<int>> pathSum(TreeNode* root, int sum) { vector<vector<int>> res; vector<int> curr; if (!root) return res; helper(res, curr, root, sum, 0); return res; } void helper(vector<vector<int>> &res, vector<int> &curr, TreeNode* root, int sum, int total) { if (!root) return; curr.push_back(root->val); total += root->val; if (!root->left && !root->right) { if (total == sum) res.push_back(curr); curr.pop_back(); return; } helper(res, curr, root->left, sum, total); helper(res, curr, root->right, sum, total); curr.pop_back(); } };
-
Leetcode (95, 96) Unique Binary Search Trees I, II
Leetcode 96. Unique Binary Search Trees
Given n, how many structurally unique BST’s (binary search trees) that store values 1…n?
For example,
Given n = 3, there are a total of 5 unique BST’s.
class Solution { public: int numTrees(int n) { int res[n+1] = {0}; res[0] = res[1] = 1; for (int i=2; i<=n; i++) for (int j=1; j<=i; j++) res[i] += res[j-1] * res[i-j]; return res[n]; } };Leetcode 95. Unique Binary Search Trees II
Given an integer n, generate all structurally unique BST’s (binary search trees) that store values 1…n.
For example, Given n = 3, your program should return all 5 unique BST’s shown below.
1 3 3 2 1 \ / / / \ \ 3 2 1 1 3 2 / / \ \ 2 1 2 3idea: 当数组为 1，2，3，4，.. i，.. n时，基于以下原则的BST建树具有唯一性 以i为根节点的树，其左子树由[1, i-1]构成， 其右子树由[i+1, n]构成。
class Solution { public: vector<TreeNode*> help_tree(int first, int last) { vector<TreeNode*> res; for (int root=first; root<last+1; root++) { auto left = root==first ? vector<TreeNode*>{nullptr}:help_tree(first, root-1); auto right = root==last ? vector<TreeNode*>{nullptr}:help_tree(root+1, last); for (auto l:left) for (auto r:right) { TreeNode *node = new TreeNode(root); node -> left = l; node -> right = r; res.push_back(node); } } return res; } vector<TreeNode*> generateTrees(int n) { return help_tree(1, n); } };
-
Leetcode (73, 74) Matrix Series
Leetcode 73. Set Matrix Zeroes
Given a m x n matrix, if an element is 0, set its entire row and column to 0. Do it in place.
class Solution { public: void setZeroes(vector<vector<int>>& matrix) { if (matrix.empty()) return; const int m = matrix.size(); const int n = matrix[0].size(); int row[m] = {0}; int col[n] = {0}; for (int i=0; i<m; i++) for (int j=0; j<n; j++) if (matrix[i][j] == 0) { row[i] = 1; col[j] = 1; } for (int i=0; i<m; i++) if (row[i] == 1) for (int j=0; j<n; j++) matrix[i][j] = 0; for (int j=0; j<n; j++) if (col[j] == 1) for (int i=0; i<m; i++) matrix[i][j] = 0; } };Leetcode 74. Search a 2D Matrix
Write an efficient algorithm that searches for a value in an m x n matrix. This matrix has the following properties:
Integers in each row are sorted from left to right. The first integer of each row is greater than the last integer of the previous row.
For example, Consider the following matrix:
[ [1, 3, 5, 7], [10, 11, 16, 20], [23, 30, 34, 50] ]Given target = 3, return true.
class Solution { public: bool searchMatrix(vector<vector<int>>& matrix, int target) { if (matrix.empty()) return false; const int m = matrix.size(); const int n = matrix[0].size(); int col = n-1, row = 0; while(col>=0 && row<m) { if (matrix[row][col] == target) return true; else if (matrix[row][col] > target) col--; else row++; } return false; } };Leetcode 48. Rotate Image
You are given an n x n 2D matrix representing an image.
class Solution { public: void rotate(vector<vector<int>>& matrix) { if (matrix.empty()) return; const int n = matrix.size(); for (int i=0; i<n; i++) for (int j=0; j<i; j++) swap(matrix[i][j], matrix[j][i]); for (int j=0; j<n/2; j++) for (int i=0; i<n; i++) swap(matrix[i][j], matrix[i][n-1-j]); } };
-
Leetcode (69, 88, 34, 507) Math Series II
- Leetcode 69. Sqrt
- Leetcode 88. Merge Sorted Array
- Leetcode 34. Search for a Range
- Leetcode 507. Perfect Number
Leetcode 69. Sqrt
Implement int sqrt(int x).
class Solution { public: int mySqrt(int x) { long m = x; while (m*m >x) m = (m+x/m)/2; return m; } };Leetcode 88. Merge Sorted Array
Given two sorted integer arrays nums1 and nums2, merge nums2 into nums1 as one sorted array.
class Solution { public: void merge(vector<int>& nums1, int m, vector<int>& nums2, int n) { int i = m-1, j = n-1, k = m + n - 1; while (j>=0) { if (i>=0 && nums2[j] < nums1[i]) nums1[k--] = nums1[i--]; else nums1[k--] = nums2[j--]; } } };Leetcode 34. Search for a Range
Given a sorted array of integers, find the starting and ending position of a given target value.
Your algorithm’s runtime complexity must be in the order of O(log n).
If the target is not found in the array, return [-1, -1].
For example,
Given [5, 7, 7, 8, 8, 10] and target value 8,
return [3, 4].
class Solution { public: vector<int> searchRange(vector<int>& nums, int target) { vector<int> res; if (nums.empty()) return res; int left = 0, right = nums.size()-1; while (left<=right) { int mid = left + (right-left)/2; if (nums[mid] == target) { int i = mid, j = mid; while (i-1>=0 && nums[i-1]== nums[i]) i--; while (j+1<nums.size() && nums[j+1]== nums[j]) j++; return {i, j}; } else if (nums[mid] < target) left = mid+1; else right = mid-1; } return {-1, -1}; } };Leetcode 507. Perfect Number
We define the Perfect Number is a positive integer that is equal to the sum of all its positive divisors except itself.
Now, given an integer n, write a function that returns true when it is a perfect number and false when it is not.
Example:
Input: 28 Output: True Explanation: 28 = 1 + 2 + 4 + 7 + 14Note: The input number n will not exceed 100,000,000. (1e8)
class Solution { public: bool checkPerfectNumber(int num) { if (num==1) return false; int temp = sqrt(num); int sum = num-1; for (int i = 2; i <= temp; i++) { if (num%i==0) { if (i==temp && temp*temp==num) sum-=i; else sum= sum-i-num/i; } if (sum<0) return false; } return sum==0; } };
-
Leetcode (3, 70) Dynamic Programming
Leetcode 3. Longest Substring Without Repeating Characters
Given a string, find the length of the longest substring without repeating characters.
Examples:
Given “abcabcbb”, the answer is “abc”, which the length is 3.
Given “bbbbb”, the answer is “b”, with the length of 1.
Given “pwwkew”, the answer is “wke”, with the length of 3. Note that the answer must be a substring, “pwke” is a subsequence and not a substring.
class Solution { public: int lengthOfLongestSubstring(string s) { const int n = s.size(); int table[256] = {0}; int start = 0, res = 0; for (int i=0; i<n; i++) { table[s[i]]++; while (table[s[i]]>1) { table[s[start++]]--; } res = max(res, i-start+1); } return res; } };70. Climbing Stairs
You are climbing a stair case. It takes n steps to reach to the top.
Each time you can either climb 1 or 2 steps. In how many distinct ways can you climb to the top?
class Solution { public: int climbStairs(int n) { int a = 1, b = 1; while (n--) a = (b += a) - a; return a; } };