Welcome to Shanshan Blog!

Principal Component Analysis Implemented in Python

2017-01-03

DataMining

DataMining Python

Using Scikit-learn package
Without packages

Using Scikit-learn package

from sklearn.decomposition import PCA   
import numpy as np

data = np.read_csv('test.csv')
pca=PCA(n_components=3)
newData=pca.fit_transform(data) 

print pca.n_components
print pca.explained_variance_ratio_

Without packages

import numpy as np
# zero mean 零均值化，每个特征的均值都为0
def zeroMean(dataMat):
    meanVal = np.mean(dataMat, axis=0)
    newData = dataMat - meanVal
    return newData, meanVa

# pca function
def pca(dataMat, n):
    newData, meanVal = zeroMean(dataMat)
    # cov array
    covMat = np.cov(newData, rowvar= 0) # rowvar = 0 means one column presents one sample

    eigVals, eigVects = np.linalg.eig(np.mat(covMat))  # 求特征值和特征向量,特征向量是按列放的，即一列代表一个特征向量
    eigValIndice = np.argsort(eigVals)  # 对特征值从小到大排序
    n_eigValIndice = eigValIndice[-1:-(n + 1):-1]  # 最大的n个特征值的下标
    n_eigVect = eigVects[:, n_eigValIndice]  # 最大的n个特征值对应的特征向量
    lowDDataMat = newData * n_eigVect  # 低维特征空间的数据
    reconMat = (lowDDataMat * n_eigVect.T) + meanVal  # 重构数据
    return lowDDataMat, reconMat

Read All

Scikit Learn Algorithm cheat sheet

2017-01-02

DataMining

DataMining Python

This machine learning cheat sheet will help you find the right estimator for the job which is the most difficult part. The flowchart will help you check the documentation and rough guide of each estimator that will help you to know more about the problems and how to solve it.

Read All
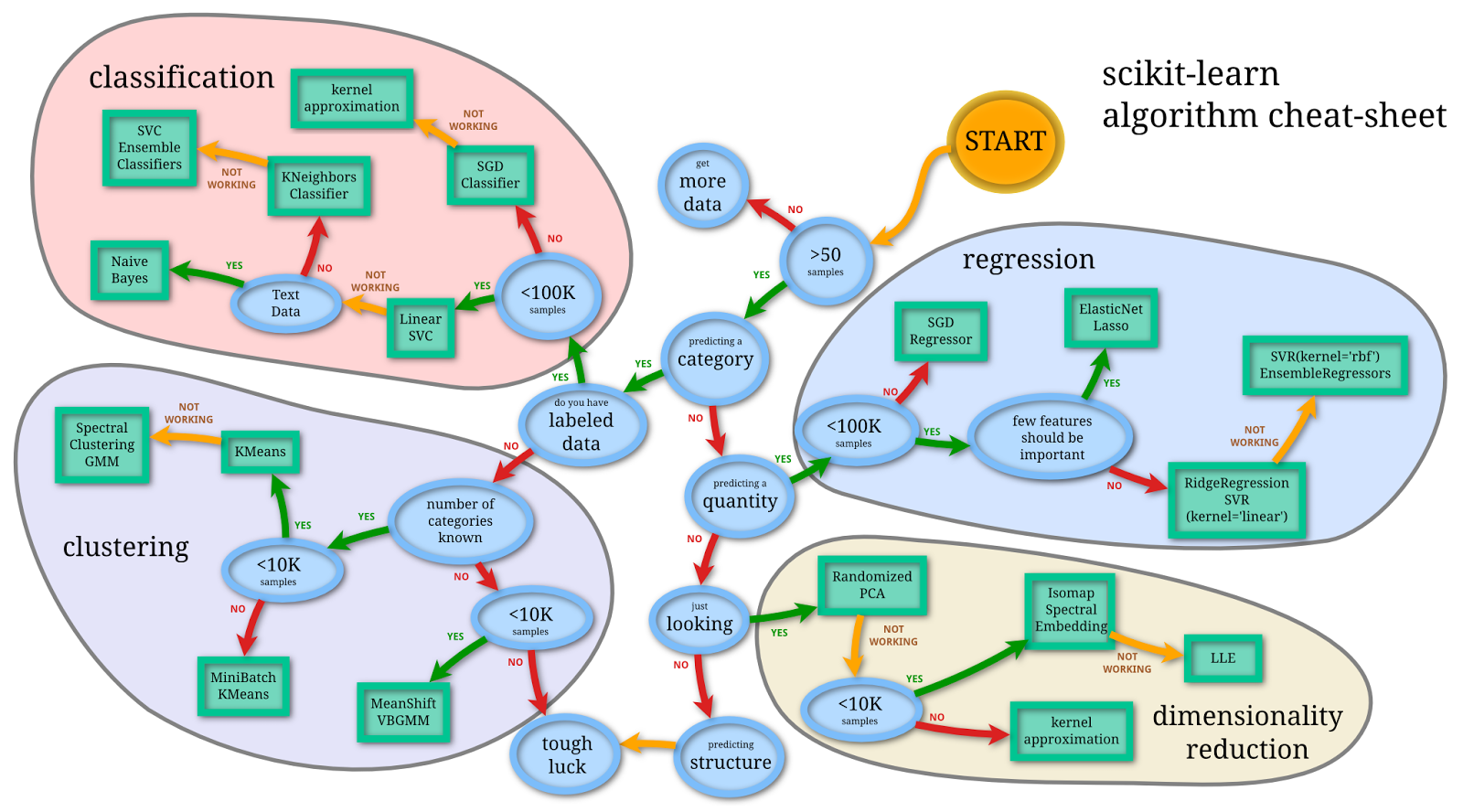
SQL Index

2017-01-01

SQL

SQL
CREATE INDEX constructs an index on the specified column(s) of the specified table. Indexes are primarily used to enhance database performance (though inappropriate use can result in slower performance).

PostgreSQL provides the index methods B-tree, hash, GiST, and GIN. Users can also define their own index methods, but that is fairly complicated.
- B-tree index
B-Tree is to handle sorted data for equation or range search, like:

< <= > >= =
```
CREATE INDEX cece_index ON cece_table (column)
```
- R-Tree index
R-Tree is suitable for two-dimensional data, like:
```
<<	&<	&>	>>	<<|		&<|		|&>
|>>		@>	<@	~=	&&
```
```
CREATE INDEX cece_index ON cece_table USING rtree (column)
```
- Hash index
Hash can only handle the “=”
```
CREATE INDEX cece_index ON cece_table USING hash (column)
```
- Gist index
There are two kinds of indexes that can be used to speed up full text searches. Note that indexes are not mandatory for full text searching, but in cases where a column is searched on a regular basis, an index is usually desirable.
```
CREATE INDEX cece_index ON cece_table USING gist(column);
```
- Multicolumn index
```
CREATE INDEX cece_index ON cece_table (column1, column2);
SELECT * FROM cece_table WHERE column1 >0 AND column2 < 0;
```
- Combining Multiple Indexes
A single index scan can only use query clauses that use the index’s columns with operators of its operator class and are joined with AND. For example, given an index on (a, b) a query condition like WHERE a = 5 AND b = 6 could use the index, but a query like WHERE a = 5 OR b = 6 could not directly use the index.
- Unique index
Force index value unque
```
CREATE UNIQUE INDEX cece_index ON cece_table (column);
```
- Indexes on Expressions
```
CREATE INDEX cece_index ON cece_table (lower(col1));
SELECT * FROM test1 WHERE lower(col1) = 'value';

SELECT * FROM people WHERE (first_name || ' ' || last_name) = 'John Smith';
CREATE INDEX people_names ON people ((first_name || ' ' || last_name));
```
- Partial index
A partial index is an index built over a subset of a table; the subset is defined by a conditional expression (called the predicate of the partial index). The index contains entries only for those table rows that satisfy the predicate. Partial indexes are a specialized feature, but there are several situations in which they are useful.
- Other index operations
```
-- Delete index
DROP cece_index
```
More details can be seen in Postgre SQL
Read All
Simple Linear Regression Model

2016-12-29

DataMining

DataMining Python
About Linear Regression

Regression is a data mining function that predicts a number. A regression task begins with a data set in which the target values are known. The simplest form of regression to visualize is linear regression with a single predictor.

Preparing Data for Linear Regression

Linear Assumption. Linear regression assumes that the relationship between your input and output is linear. It does not support anything else. This may be obvious, but it is good to remember when you have a lot of attributes. You may need to transform data to make the relationship linear (e.g. log transform for an exponential relationship).

Remove Noise. Linear regression assumes that your input and output variables are not noisy. Consider using data cleaning operations that let you better expose and clarify the signal in your data. This is most important for the output variable and you want to remove outliers in the output variable (y) if possible.

Remove Collinearity. Linear regression will over-fit your data when you have highly correlated input variables. Consider calculating pairwise correlations for your input data and removing the most correlated.

Gaussian Distributions. Linear regression will make more reliable predictions if your input and output variables have a Gaussian distribution. You may get some benefit using transforms (e.g. log or BoxCox) on you variables to make their distribution more Gaussian looking.

Rescale Inputs: Linear regression will often make more reliable predictions if you rescale input variables using standardization or normalization.

How does Linear Regression Work?

In mathematical notion, if \hat{y} is the predicted value.

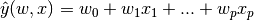
In scikit-linear package, designate the vector w = (w_1,…, w_p) as coef_ and w_0 as intercept_.

LinearRegression fits a linear model with coefficients w = (w_1, …, w_p) to minimize the residual sum of squares between the observed responses in the dataset, and the responses predicted by the linear approximation. Mathematically it solves a problem of the form:

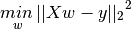
Test Linear Regression

Root Mean Squared Error

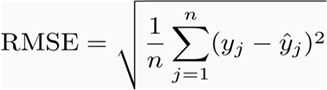
Mean Absolute Error
Read All

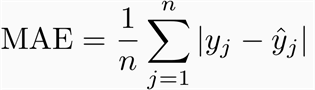
SQL Paritioning

2016-12-27

SQL

The example is test in Postgre SQL.

Step 1: Create the big table

CREATE TABLE student (student_id bigserial, name varchar(32), score smallint);

Step 2: Create the sub Table

CREATE TABLE student_qualified (CHECK (score >= 60 )) INHERITS (student) ;
CREATE TABLE student_nqualified (CHECK (score < 60)) INHERITS (student) ;```

table student_qualified and student_nqualified will cover inherits the big table.

Step 3: Define the rule or Trigger

Even we define the CHECK Condition, when insert new data into table student, Postgre SQL couldnot find the subtable. So we need to create the rule to make sure data inserted into the correct partition.

Firstly, let us define the Rule

```sql
CREATE OR REPLACE RULE insert_student_qualified 
AS ON INSERT TO student 
       WHERE score >= 60
       DO INSTEAD
       INSERT INTO student_qualified VALUES(NEW.*);

CREATE OR REPLACE RULE insert_student_nqualified 
AS ON INSERT TO student 
       WHERE score < 60
       DO INSTEAD
       INSERT INTO student_nqualified VALUES(NEW.*);

Step 4: insert some data into the table

INSERT INTO student (name,score) VALUES('Jim',77);
INSERT INTO student (name,score) VALUES('Frank',56);
INSERT INTO student (name,score) VALUES('Bean',88);
INSERT INTO student (name,score) VALUES('John',47);
INSERT INTO student (name,score) VALUES('Albert','87');
INSERT INTO student (name,score) VALUES('Joey','60');

Step 5: show the data distribution

SELECT p.relname,c.tableoid,c.* 
FROM student c, pg_class p
WHERE c.tableoid = p.oid

We also define the Trigger to make conditions for insertion.

CREATE OR REPLACE FUNCTION student_insert_trigger()
RETURNS TRIGGER AS 
$$
BEGIN
     IF(NEW.score >= 60) THEN
         INSERT INTO student_qualified VALUES (NEW.*);
     ELSE 
         INSERT INTO student_nqualified VALUES (NEW.*);
     END IF;
     RETURN NULL;
END;
$$
LANGUAGE plpgsql ;

CREATE TRIGGER insert_student 
    BEFORE INSERT ON student
    FOR EACH row
    EXECUTE PROCEDURE student_insert_trigger() ;

If the trigger doesnot work, you have to open the trigger, in postgresql.conf, to define

track_functions = all

In the end, I test the create table and select operations status in partitioning, compared with the original big table. Even the speed to create table is quite slow, but the selection is significantly quicker than the original table.

Read All

Feature Selection in Data Mining

2016-12-25

DataMining

DataMining
Feature Selection

Scikit-learn provides some feature selection methods for data mining.

Method 1: Remove features with low variance

For discrete values, for example, one feature with two values ( 0 and 1 ), if there are more than 80% samples with the same values, then the feature is invalid, so we remove this feature.

As an example, suppose that we have a dataset with boolean features, and we want to remove all features that are either one or zero (on or off) in more than 80% of the samples. Boolean features are Bernoulli random variables, and the variance of such variables is given by

VAR[X] = p(1-p)

here we select p as 0.8
```
from sklearn.feature_selection import VarianceThreshold

# varriance threshould
X = [[0, 0, 1], [0, 1, 0], [1, 0, 0], [0, 1, 1], [0, 1, 0], [0, 1, 1]]
sel = VarianceThreshold(threshold=(.8*(1-.8)))
print sel.fit_transform(X)
```
the result removes the first column, which has a probability p = 5/6 > .8 of containing a zero.

Method 2: Univariate feature selection

Univariate feature selection works by selecting the best features based on univariate statistical tests. It can be seen as a preprocessing step to an estimator.

In scikit-learn, it includes:
- SelectKBest: removes all but the k highest scoring features
- SelectPercentile: removes all but a user-specified highest scoring percentage of features
- GenericUnivariateSelect: allows to perform univariate feature selection with a configurable strategy.
SelectKBest method example
```
from sklearn.datasets import load_iris
from sklearn.feature_selection import SelectKBest
from sklearn.feature_selection import chi2

iris = load_iris()
x, y = iris.data, iris.target
print x.shape
x_new = SelectKBest(chi2, k=2).fit_transform(x, y)
print x_new.shape
```
For the object, we can
- For regression: f_regression, mutual_info_regression
- For classification: chi2, f_classif, mutual_info_classif
The methods based on F-test estimate the degree of linear dependency between two random variables. On the other hand, mutual information methods can capture any kind of statistical dependency, but being nonparametric, they require more samples for accurate estimation.

f_regression will calculate the p-value of features. Smaller noise, higher relationship lower p-value.

mutual_info_regression and mutual_info_classif are mutual information, sensitive to the discrete info.

Method 3: Feature selection using SelectFromModel

SelectFromModel is a meta-transformer that can be used along with any estimator that has a coef_ or feature_importances_ attribute after fitting. The features are considered unimportant and removed, if the corresponding coef_ or feature_importances_ values are below the provided threshold parameter. Apart from specifying the threshold numerically, there are built-in heuristics for finding a threshold using a string argument. Available heuristics are “mean”, “median” and float multiples of these like “0.1*mean”.
- L1-based feature selection
Linear models penalized with the L1 norm have sparse solutions: many of their estimated coefficients are zero. When the goal is to reduce the dimensionality of the data to use with another classifier
```
# selection from model : linear model
from sklearn.svm import LinearSVC
from sklearn.feature_selection import SelectFromModel
lsvc = LinearSVC(C=0.01, penalty="l1", dual=False).fit(x, y)
model = SelectFromModel(lsvc, prefit=True)
x_new = model.transform(x)
print x_new.shape
```
Read All

20/38

Welcome to Shanshan Blog!

Principal Component Analysis Implemented in Python

Using Scikit-learn package

Without packages

Scikit Learn Algorithm cheat sheet

SQL Index

Simple Linear Regression Model

About Linear Regression

Preparing Data for Linear Regression

How does Linear Regression Work?

Test Linear Regression

SQL Paritioning

Feature Selection in Data Mining