Welcome to Shanshan Blog!
-
Code Jam to I/O 2017 for Women Problem B Understudies
Problem
You are a casting director for an upcoming musical. The musical has N roles, and for each role, you want to cast two performers: one primary performer and one understudy. A primary performer or understudy trains for only one particular role, and the job of the understudy is to play the role if the primary performer becomes unavailable. At least one of the two performers for each role must be available for the show to succeed.
You have selected 2N performers to be in the musical. They are all quite talented, and any of them can be cast as a primary performer or understudy for any of the roles. However, you are worried that some of them may be tempted to run away to join the cast of Hamiltonian!, the smash hit musical about quantum mechanics, before your show opens. Luckily, you are an excellent judge of character. You know that the i-th performer has a probability Pi of becoming unavailable. (These probabilities are all independent of each other, and a given performer has their probability regardless of their assigned role or whether they are a primary performer or understudy.)
You wish to assign one primary performer and one understudy for each role in a way that maximizes the probability that the show will succeed. That is, you want to minimize the probability that there will be at least one role for which the primary performer and understudy both become unavailable.
If you make optimal casting choices, what is the probability that your show will succeed?
Input and Output
Input
The first line of the input gives the number of test cases, T. T test cases follow; each consists of two lines. The first line contains a single integer N: the number of roles. The second line contains 2N rational numbers Pi; the i-th of these gives the probability that the i-th performer will become unavailable for your show. All of these probabilities are specified to exactly four decimal places of precision.
Output
For each test case, output one line containing Case #x: y, where x is the test case number (starting from 1) and y is the probability that your show will succeed. y will be considered correct if it is within an absolute or relative error of 10-6 of the correct answer. See the FAQ for an explanation of what that means, and what formats of real numbers we accept.
Limits
1 ≤ T ≤ 100.
0.0000 ≤ Pi ≤ 1.0000, for all i.
Small dataset
1 ≤ N ≤ 4.
Large dataset
1 ≤ N ≤ 40.
Sample
Input 3 2 0.2500 0.5000 0.5000 0.2500 3 0.0000 0.0000 0.0000 0.0009 0.0013 0.1776 1 1.0000 0.1234 Output Case #1: 0.765625 Case #2: 1.000000 Case #3: 0.876600In sample case #1, one optimal casting choice is to make the two 0.5000 performers leads for the two roles, and the two 0.2500 performers understudies. For a given role, the probability that both performers will become unavailable is 0.5 × 0.25 = 0.125. So the probability that a role will be filled by at least one of its actors is 1 - 0.125 = 0.875. The probability that both roles will be filled (and thus that the show will succeed) is 0.875 × 0.875 = 0.765625.
If we instead cast the two 0.5000 performers for one role and the two 0.2500 performers for the other role, the probability of success would be (1 - 0.50 × 0.50) × (1 - 0.25 × 0.25) = 0.703125, which is lower.
In sample case #2, the show will succeed for sure as long as you cast exactly one of the 0.0000 performers (who will never become unavailable) in each role.
In sample case #3, the 1.0000 performer will always become unavailable, so the probability of success is equal to 1 minus the probability that the other performer will become unavailable.
Codes
#include <iostream> #include <algorithm> #include <vector> using namespace std; int main() { freopen("C:\\Users\\fushanshan\\Downloads\\B-large-practice.in","r",stdin); freopen("C:\\Users\\fushanshan\\Downloads\\B-large-attempt0.out","w",stdout); int num, N; double a; cin >> num; for (int i = 0; i < num; i++) { cout << "Case #" << i + 1 << ": "; cin >> N; vector<double> v; for (int j = 0; j < 2*N; j++) { cin >> a; v.push_back(a); } sort(v.begin(), v.end()); double res = 1; for (int j = 0; j < N; j++) { res *= (1 - v.at(j) * v.at(2 * N-j-1)); } cout << res << endl; v.clear(); } return 0; }
-
Code Jam to I/O 2017 for Women Problem A Ticket Trouble
Problem
A group of F friends is attending a conference held at an amphitheater, and they have bought tickets to see a concert there afterwards. The amphitheater is a grid of seats with S rows and S columns. For each seat, the amphitheater has sold a single ticket (although some of the tickets might not have been sold to this group of friends). Each ticket is normally labeled with a pair of integers giving the row and column numbers of one seat, in that order. For example, a ticket might normally say (2, 1), meaning row 2, column 1, or (2, 2), meaning row 2, column 2.
When the tickets were printed, there was a malfunction, and the two numbers in each pair always came out in sorted (that is, nondecreasing) order! So, for example, a ticket labeled (1, 2) might actually be for the seat in row 1, column 2, or it might actually be for the seat in row 2, column 1. If two friends have tickets labeled (1, 2), then one must actually be for row 1, column 2, and the other must actually be for row 2, column 1.
The friends will consult the box office on the day of the concert to find out what their actual seat numbers are, but for now, it is unclear! Given the printed pairs on the tickets, what is the largest possible number of the friends that could actually be seated all in the same-numbered row of seats? (The friends do not necessarily need to be seated in consecutive seats in that row.)
Input and Output
Input
The first line of the input gives the number of test cases, T. T test cases follow. Each begins with one line with two integers F and S, representing the number of friends and the dimension of the grid of seats. Then, F more lines follow. The i-th of those lines has two integers Ai and Bi, representing the two numbers printed on the i-th friend’s ticket.
Output
For each test case, output one line containing Case #x: y, where x is the test case number (starting from 1) and y is largest possible number of the friends that could actually be seated all in the same-numbered row of seats.
Limits
F ≤ S2.
1 ≤ Ai ≤ Bi ≤ S, for all i.
No pair appears more than twice in a test case.
No pair containing the same number twice appears more than once in a test case.
Small dataset
1 ≤ T ≤ 50.
2 ≤ F ≤ 3.
2 ≤ S ≤ 3.
Large dataset
1 ≤ T ≤ 100.
2 ≤ F ≤ 100.
2 ≤ S ≤ 100.
Sample
Input 3 2 3 1 2 1 2 3 3 1 2 2 3 2 2 3 3 1 1 2 2 1 2 Output Case #1: 1 Case #2: 3 Case #3: 2In sample case #1, one ticket must actually be for row 1, column 2, and the other must actually be for row 2, column 1, even though we do not know which is which. So we know that the friends are not seated in the same row, and the largest number of friends in any row is 1. Also note that the seats have a third row and column, but none of the tickets use the third row or column.
In sample case #2, one of the tickets is definitely for seat 2 in row 2, and it is possible that two of the other tickets could be for seats 1 and 3 in row 2. So there may be as many as 3 friends in the same row.
In sample case #3, either there are two friends in row 1 and one in row 2, or there are two friends in row 2 and one in row 1. In either case, the answer is 2.
Codes
#include <iostream> #include <unordered_map> struct pair_hash { template <class T1, class T2> std::size_t operator () (const std::pair<T1,T2> &p) const { auto h1 = std::hash<T1>{}(p.first); auto h2 = std::hash<T2>{}(p.second); return h1 ^ h2; } }; using namespace std; int main() { freopen("C:\\Users\\fushanshan\\Downloads\\A-large-practice.in","r",stdin); freopen("C:\\Users\\fushanshan\\Downloads\\A-large-attempt0.out","w",stdout); int num, F, S, a, b; unordered_map<int, int> res; unordered_map<pair<int, int>, int, pair_hash> temp; cin >> num; for (int i = 0; i < num; i++) { cout << "Case #" << i + 1 << ": "; cin >> F >> S; for (int j = 0; j < F; j++) { cin >> a >> b; if (a == b) res[a] += 1; else { pair<int, int> temp_P = (a > b) ? make_pair(a, b) : make_pair(b, a); if (temp[temp_P] == 0) { res[a] += 1; res[b] += 1; temp[temp_P] += 1; } } } int ans = 0; for( int j = 1; j <= S; j++){ if (ans < res[j]) ans = res[j]; } cout << ans << endl; res.clear();temp.clear(); } return 0; }
-
Leetcode (116, 117) Populating Next Right Pointers in Each Node I, II
- Leetcode 116. Populating Next Right Pointers in Each Node
- Leetcode 117. Populating Next Right Pointers in Each Node II
Populating Next Right Pointers in Each Node
Leetcode 116. Populating Next Right Pointers in Each Node
Given a binary tree
struct TreeLinkNode { TreeLinkNode *left; TreeLinkNode *right; TreeLinkNode *next; }Populate each next pointer to point to its next right node. If there is no next right node, the next pointer should be set to NULL.
Initially, all next pointers are set to NULL.
Note:
-
You may only use constant extra space.
-
You may assume that it is a perfect binary tree (ie, all leaves are at the same level, and every parent has two children).
For example, Given the following perfect binary tree,
1 / \ 2 3 / \ / \ 4 5 6 7After calling your function, the tree should look like:
1 -> NULL / \ 2 -> 3 -> NULL / \ / \ 4->5->6->7 -> NULL/** * Definition for binary tree with next pointer. * struct TreeLinkNode { * int val; * TreeLinkNode *left, *right, *next; * TreeLinkNode(int x) : val(x), left(NULL), right(NULL), next(NULL) {} * }; */ class Solution { public: void connect(TreeLinkNode *root) { if (!root) return; if (root -> left) { root-> left -> next = root -> right; if (root -> next) root -> right -> next = root -> next -> left; } connect(root -> left); connect(root -> right); } };Leetcode 117. Populating Next Right Pointers in Each Node II
Follow up for problem “Populating Next Right Pointers in Each Node”.
What if the given tree could be any binary tree? Would your previous solution still work?
Note:
You may only use constant extra space. For example, Given the following binary tree,
1 / \ 2 3 / \ \ 4 5 7After calling your function, the tree should look like:
1 -> NULL / \ 2 -> 3 -> NULL / \ \ 4-> 5 -> 7 -> NULL ```cpp /** * Definition for binary tree with next pointer. * struct TreeLinkNode { * int val; * TreeLinkNode *left, *right, *next; * TreeLinkNode(int x) : val(x), left(NULL), right(NULL), next(NULL) {} * }; */ class Solution { public: void connect(TreeLinkNode *root) { if (!root) return; TreeLinkNode dummy(INT_MIN); for (TreeLinkNode *cur = root, *pre = &dummy; cur; cur = cur->next) { if (cur -> left) { pre -> next = cur -> left; pre = pre -> next; } if (cur -> right) { pre -> next = cur -> right; pre = pre -> next; } } connect(dummy.next); } };
-
Leetcode (118, 119) Pascal's Triangle I, II
Pascal’s Triangle
Leetcode 118. Pascal’s Triangle
Given numRows, generate the first numRows of Pascal’s triangle.
For example, given numRows = 5, Return
[ [1], [1,1], [1,2,1], [1,3,3,1], [1,4,6,4,1] ]class Solution { public: vector<vector<int>> generate(int numRows) { vector<vector<int>> res; for (int i = 0; i < numRows; i++) { res.push_back(vector<int>(i+1, 1)); for (int j = 1; j < i; j++) res[i][j] = res[i-1][j-1] + res[i-1][j]; } return res; } };Leetcode 119. Pascal’s Triangle II
Given a triangle, find the minimum path sum from top to bottom. Each step you may move to adjacent numbers on the row below.
For example, given the following triangle
[ [2], [3,4], [6,5,7], [4,1,8,3] ]The minimum path sum from top to bottom is 11 (i.e., 2 + 3 + 5 + 1 = 11).
Note: Bonus point if you are able to do this using only O(n) extra space, where n is the total number of rows in the triangle.
class Solution { public: vector<int> getRow(int rowIndex) { vector<int> res(rowIndex + 1); res[0] = 1; for (int i = 0; i <= rowIndex; i++) for (int j = i; j > 0; j--) res[j] = res[j] + res[j-1]; return res; } };
-
Leetcode (84, 85) Rectangle
Leetcode Rectangle
Leetcode 84. Largest Rectangle in Histogram
Given n non-negative integers representing the histogram’s bar height where the width of each bar is 1, find the area of largest rectangle in the histogram.
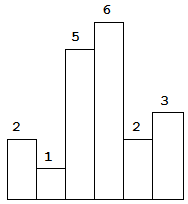
Above is a histogram where width of each bar is 1, given height = [2,1,5,6,2,3].
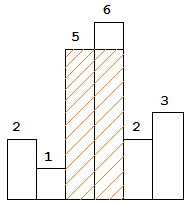
The largest rectangle is shown in the shaded area, which has area = 10 unit.
For example,
Given heights = [2,1,5,6,2,3],
return 10.
class Solution { public: int largestRectangleArea(vector<int>& heights) { int res = 0; heights.push_back(0); vector<int> index; for (int i = 0; i < heights.size(); i++) { while (index.size() > 0 && heights[index.back()] >= heights[i]) { int h = heights[index.back()]; index.pop_back(); int idx = index.size() > 0 ? index.back():-1; if (h * (i-idx-1) > res) res = h * (i-idx-1); } index.push_back(i); } return res; } };Leetcode 85. Maximal Rectangle
Given a 2D binary matrix filled with 0’s and 1’s, find the largest rectangle containing only 1’s and return its area.
For example, given the following matrix:
1 0 1 0 0 1 0 1 1 1 1 1 1 1 1 1 0 0 1 0Return 6.
class Solution { public: int maximalRectangle(vector<vector<char>>& matrix) { if (matrix.size() == 0 || matrix[0].size() == 0) return 0; int m = matrix.size(), n = matrix[0].size(), res = 0; vector<int> left(n, 0), right(n, n), height(n, 0); for (int i = 0; i < m; i++) { int cur_left = 0, cur_right = n; for (int j = 0; j < n; j++) height[j] = matrix[i][j] == '1' ? height[j]+1 : 0; for (int j = 0; j < n; j++) { left[j] = matrix[i][j] == '1' ? max(left[j], cur_left) : 0; cur_left = matrix[i][j] == '1' ? cur_left : j+1; } for (int j = n-1; j >= 0; j--) { right[j] = matrix[i][j] == '1' ? min(right[j], cur_right) : n; cur_right = matrix[i][j] == '1' ? cur_right : j; } for (int j = 0; j < n; j++) res = max(res, (right[j]- left[j])*height[j]); } return res; } };
-
Leetcode (485) Math Series III
Leetcode Math Series III
Leetcode 485. Max Consecutive Ones
Given a binary array, find the maximum number of consecutive 1s in this array.
Example 1:
Input: [1,1,0,1,1,1] Output: 3 Explanation: The first two digits or the last three digits are consecutive 1s. The maximum number of consecutive 1s is 3.Note:
-
The input array will only contain 0 and 1.
-
The length of input array is a positive integer and will not exceed 10,000
class Solution { public: int findMaxConsecutiveOnes(vector<int>& nums) { if (nums.empty()) return 0; int res = 0, begin=0, last =-1; for (int i = 0; i<nums.size();i++) { if (nums[i]==0) { res = max(res, last-begin+1); begin = i+1; last = i; } else { last++; } } return max(res, last-begin+1); } };
-