Welcome to Shanshan Blog!
-
Heap Operations in Python
Heap Operation
In python, heapq module offers some operations related to heap.
# -*- coding:utf-8 -*- # 使用python自带的包进行heap的相关操作 from heapq import * from random import shuffle # 定义堆,建堆 x=[1,2,3,4,5,6] x = shuffle(x) heap = [] for i in x: heappush(heap, i) print heap # 增加要素 heappush(heap, 8) print heap # 删除要素 print heappop(heap) print heap # 生成堆 x=[1,4,2,3,5,4] heapify(x) print x
-
Odd_Even Sort and Implementation in Python
Odd Even Sort
It functions by comparing all odd/even indexed pairs of adjacent elements in the list and, if a pair is in the wrong order (the first is larger than the second) the elements are switched. The next step repeats this for even/odd indexed pairs (of adjacent elements). Then it alternates between odd/even and even/odd steps until the list is sorted.
Example
Given a list [6 2 4 1 5 9]
a. Odd turn: [2 6 1 4 5 9] b. Even turn: [2 1 6 4 5 9] c. Odd turn: [1 2 4 6 5 9] d. Even turn: [1 2 4 5 6 9]Complexity

Pseudocode
algorithm quicksort(A, lo, hi) is if lo < hi then p := partition(A, lo, hi) quicksort(A, lo, p – 1) quicksort(A, p + 1, hi) algorithm partition(A, lo, hi) is pivot := A[hi] i := lo // place for swapping for j := lo to hi – 1 do if A[j] ≤ pivot then swap A[i] with A[j] i := i + 1 swap A[i] with A[hi] return iImplementation in Python
# -*- coding:utf-8 -*- # 又一个比较性质的排序,基本思路是奇数列排一趟序,偶数列排一趟序,再奇数排,再偶数排,直到全部有序 def odd_even_sort(l): flag = True flag = True for i in range(len(l) - 1): if flag: flag = False for j in range(1, len(l), 2): if l[j] > l[j + 1]: flag = True l[j], l[j + 1] = l[j + 1], l[j] for j in range(0, len(l) - 1, 2): if l[j] > l[j + 1]: flag = True l[j], l[j + 1] = l[j + 1], l[j] def main(): l = [2, 3, 4, 1, 7, 3, 8, 1100, 282828, 1, 20, 0] li = odd_even_sort(l) print li main()
-
Insertion Sort and Implementation in Python
Insertion Sort
Insertion sort is a simple sorting algorithm that builds the final sorted array (or list) one item at a time. In this post, we only present the
Complexity
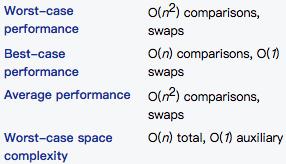
Example
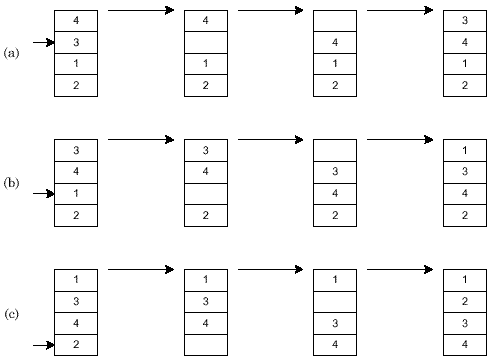
Pseudocode
for i ← 1 to length(A) j ← i while j > 0 and A[j-1] > A[j] swap A[j] and A[j-1] j ← j - 1 end while end forImplementation in Python
# -*- coding:utf-8 -*- # 插入排序就是每一步都将一个待排数据按其大小插入到已经排序的数据中的适当位置,直到全部插入完毕。 # 插入排序方法分直接插入排序和折半插入排序两种,这里只介绍直接插入排序 def insert_sort(l): for i in range(1,len(l)): if (l[i]<l[i-1]): temp = l[i] j = i while (j>0 and l[j-1]>temp): l[j] = l[j-1] j = j-1 l[j] = temp return l def main(): l = [2, 3, 4, 1, 7, 3, 8, 1100, 282828, 1, 20, 0] li = insert_sort(l) print li main()
-
Selection Sort and Implementation in Python
Selection Sort
The algorithm divides the input list into two parts: the sublist of items already sorted, which is built up from left to right at the front (left) of the list, and the sublist of items remaining to be sorted that occupy the rest of the list. Initially, the sorted sublist is empty and the unsorted sublist is the entire input list.
Complexity
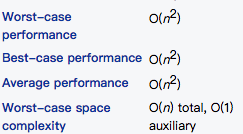
Example
64 25 12 22 11 // this is the initial, starting state of the array 11 25 12 22 64 // sorted sublist = {11} 11 12 25 22 64 // sorted sublist = {11, 12} 11 12 22 25 64 // sorted sublist = {11, 12, 22} 11 12 22 25 64 // sorted sublist = {11, 12, 22, 25} 11 12 22 25 64 // sorted sublist = {11, 12, 22, 25, 64}Implementation in Python
# -*- coding:utf-8 -*- # 顾名思意,就是直接从待排序数组里选择一个最小(或最大)的数字,每次都拿一个最小数字出来, # 顺序放入新数组,直到全部拿完 def selection_sort(l): for i in range(0, len(l)): min_index = i min_num = l[i] for j in range(i+1, len(l)): if (l[j] < min_num): min_index = j min_num = l[j] l[min_index] = l[i] l[i] = min_num return l def main(): l = [2, 3, 4, 1, 7, 3, 8, 1100, 282828, 1, 20, 0] li = selection_sort(l) print li main()
-
Merge Sort and Implementation in Python
Merge Sort
Conceptually, a merge sort works as follows:
a. Divide the unsorted list into n sublists, each containing 1 element (a list of 1 element is considered sorted).
b. Repeatedly merge sublists to produce new sorted sublists until there is only 1 sublist remaining. This will be the sorted list.
Complexity
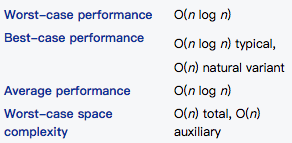
Example
a. Given unsorted list: [6 2 4 1 5 9] b. Seperate: [2 6] [1 4] [5 9] c. Merge them: [1 2 4 6] [5 9] d. Continue merge: [1 2 4 5 6 9]Implementation in Python
# -*- coding:utf-8 -*- # 顾名思意,就是直接从待排序数组里选择一个最小(或最大)的数字,每次都拿一个最小数字出来, # 顺序放入新数组,直到全部拿完 # 再简单点,对着一群数组说,你们谁最小出列,站到最后边 # 然后继续对剩余的无序数组说,你们谁最小出列,站到最后边 # 再继续刚才的操作,一直到最后一个,继续站到最后边,现在数组有序了,从小到大 import copy def merge_sort(l): res = [] if (len(l) <=1): return l mid = len(l) / 2 left_l = merge_sort(l[: mid]) right_l = merge_sort(l[mid:len(l)]) while (len(left_l)>0 and len(right_l)): if (left_l[0]>right_l[0]): res.append(right_l.pop(0)) else: res.append(left_l.pop(0)) if (len(left_l)>0): res.extend(merge_sort(left_l)) else: res.extend(merge_sort(right_l)) return res def main(): l = [2, 3, 4, 1, 7, 3, 8, 1100, 282828, 1, 20, 0] li = merge_sort(l) print li main()
-
Bubble Sort and Implementation in Python
Bubble Sort
Bubble sort, sometimes referred to as sinking sort, is a simple sorting algorithm that repeatedly steps through the list to be sorted, compares each pair of adjacent items and swaps them if they are in the wrong order.
Complexity

Example
First Pass ( 5 1 4 2 8 ) to ( 1 5 4 2 8 ), Here, algorithm compares the first two elements, and swaps since 5 > 1. ( 1 5 4 2 8 ) to ( 1 4 5 2 8 ), Swap since 5 > 4 ( 1 4 5 2 8 ) to ( 1 4 2 5 8 ), Swap since 5 > 2 ( 1 4 2 5 8 ) to ( 1 4 2 5 8 ), Now, since these elements are already in order (8 > 5), algorithm does not swap them. Second Pass ( 1 4 2 5 8 ) to ( 1 4 2 5 8 ) ( 1 4 2 5 8 ) to ( 1 2 4 5 8 ), Swap since 4 > 2 ( 1 2 4 5 8 ) to ( 1 2 4 5 8 ) ( 1 2 4 5 8 ) to ( 1 2 4 5 8 ) Now, the array is already sorted, but the algorithm does not know if it is completed. The algorithm needs one whole pass without any swap to know it is sorted. Third Pass ( 1 2 4 5 8 ) to ( 1 2 4 5 8 ) ( 1 2 4 5 8 ) to ( 1 2 4 5 8 ) ( 1 2 4 5 8 ) to ( 1 2 4 5 8 ) ( 1 2 4 5 8 ) to ( 1 2 4 5 8 )Pseudocode
procedure bubbleSort( A : list of sortable items ) n = length(A) repeat swapped = false for i = 1 to n-1 inclusive do /* if this pair is out of order */ if A[i-1] > A[i] then /* swap them and remember something changed */ swap( A[i-1], A[i] ) swapped = true end if end for until not swapped end procedureImplementation in Python
# -*- coding:utf-8 -*- # 原理是临近的数字两两进行比较,按照从小到大或者从大到小的顺序进行交换, # 这样一趟过去后,最大或最小的数字被交换到了最后一位, # 然后再从头开始进行两两比较交换,直到倒数第二位时结束 def bubble_sort(l): len_l = len(l) for i in range(0, len_l-1): for j in range(i, len_l): if (l[i] > l[j]): l[i], l[j] = l[j], l[i] return l def main(): l = [2, 3, 4, 1, 7, 3, 8, 1100, 282828, 1, 20, 0] li = bubble_sort(l) print li main()