Welcome to Shanshan Blog!
-
计算广告学 笔记6 广告交易市场
- 课时31 广告交易市场
- 课时32 实时竞价
- 课时33 Cookie Mapping
- 课时35 Demand Side Platform
- 课时36 DSP流量预测
- 课时37 DSP点击价值估计
- 课时38 DSP重定向
- 课时39 需求端推荐方法
- 课时40 广告流量交易方式
课程地址:计算广告学
课时31 广告交易市场
广告交易平台:
关键特征:用实时竞价(RTB)方式链接广告和(上文,用户);按照展示上的竞价收取广告主费用
课时32 实时竞价
-
实时竞价 Real time bidding(RTB) RTB 的流程可以分为cookie mapping 和Ad
-
call两个过程 cookie mapping的作用是沟通Adx和DSP,使得两边都了解有哪些cookie ad call是正式的广告投放
这里面有一些潜在的风险,如有些公司加入RTB目标就是用非常廉价的方式拿到用户数据,而非投广告。并且,由于多了一次访问请求返回,会增加浏览者的网页响应时间。对于用户来说,等待大约多了 100ms,这样对用户 ctr 是有影响的,并且增加了Demand端的成本和server的成本
课时33 Cookie Mapping
第一个例子:DSP和adExchange 之间进行Cookie Mapping,由DSP发起,在广告主控制的网站上发起,mapping表存在DSP端,目的是为了获取DSP cookie和Adx cookie之间的对应关系。 当用户浏览含有DSP代码的网页的时候,网页向DSP提出询问请求, DSP cookie服务确认该网页用户的cookie很久没有更新过了,就向该页面提出我需要同步你的cookie 然后该页面将相关信息提交给ad exchange,xid= adx cookie id(这个不明白,dsp端是怎么获得的,是否xid是代表exchange的ID),did(demand cookie id),dck = demand cookie adx把对应的xck= adx cookie返回给DSP端 到此为止,DSP端就把自己的cookie和ADX端的cookie对应起来了,存在DSP端的表里面。
当以后广告需求产生的时候,ADX把xck发给DSP,DSP在自己的表里查,这个人是不是我要的,是要的,我再出价购买。
第二个例子:
网站想了解访问自己网站用户的更多消息,或者用户的分类,标签等等,所以需要向dmp询问 网站自己存自己的用户cookie和dmp cookie的映射 如果网站想了解用户,就先查表,获得dmp cookie,然后向dmp发送这个用户的dmp cookie,dmp就返回这个用户标签等等
课时34 Supply Side Platform
对于媒体,有四种变现模式:
-
大媒体,直接GD销售,变现能力最高(按天销售)
-
分类流量后,按照GD销售(按CPM销售,target)
-
流量托管给广告联盟
-
RTB
SSP等于是同时做这4个,收益统一管理,灵活接入多种变现方式。Sell-Side Platform,即供应方平台。供应方平台能够让网络媒体也介入广告交易,从而使它们的库存广告可用。通过这一平台,网络媒体希望他们的库存广告可以获得最高的有效每千次展示费用,而不必以低价销售出去。
课时35 Demand Side Platform
需求方平台 Demand Side Platform:需求方平台允许广告客户和广告机构更方便地访问,以及更有效地购买广告库存,因为该平台汇集了各种广告交易平台的库存。
目的:Allows digital advertisers to manage multiple ad exchange and data exchange accounts through one interface
关键特征:
定制化用户划分
跨媒体流量采购
通过ROI估计来支持RTB
代表:InviteMedia, MediaMath
课时36 DSP流量预测
开放的问题:如何利用历史投放数据估计流量?(没有公认的合适的方法)
课时37 DSP点击价值估计
点击价格估计的应用场景:
-
DSP的实时出价
-
广告网络的出价工具
-
智能定价:广告网络方需要对不同质量的流量估计一个相对的价值,方便对广告主打折(比如说上下文的5折,搜索引擎的全价)。
这个问题作为机器学习的挑战:
-
数据非常稀疏
-
与广告主类型强烈相关的行为模式 点击价值估计若干原则
模型估计时,用较大的bias换较小的variance,已达到稳健估计的目的
充分利用广告商类型的层级结构,以及转化流程上的特征
课时38 DSP重定向
DSP:DSP大致有3个功能,重定向、人群标签、相似用户。
重定向的分类:
1、网站重定向:根据浏览的网站的内容进行重定向。对做品牌的够用了。比如进入过京东商城,到别的网站去给你推荐京东的东西。
2、搜索重定向: 根据搜索行为
3、个性化重定向:
根据浏览、关注、购买等各阶段,进行适合的推荐。 个性化重定向:粒度是商品。没下单,激励下单,已下单,推荐相关。
和推荐不同的是,推荐是按照上下文推荐,比如说前一个页看到,而这个主要是给user打标签
推荐算法概述:
1、协同过滤:
2、基于内容方法
3、推荐算法的本质? 对{user、a}的co-occurence这一稀疏矩阵的参数或非参数化的描述。
4、推荐算法选择的关键:探索较合适的bias和variance的平衡,以适应问题的数据稀疏性
课时39 需求端推荐方法
课时40 广告流量交易方式
广告交易市场中的问题还没有形成系统的体系,所以主要介绍概念,算法和技术还不成定论。
广告流量交易方式
1.程序交易(programmatic trade) 实时竞价(RTBS RTBD)、Adx、优选、网络优化、组合优化、ad network
2.优先销售(premium sale) CPT、Guaranteed Delivery担保投送、Ad server 趋势是市场向demand方向发展,并且越来越侧重于程序购买
-
计算广告学 笔记5.2 搜索广告
课程地址:计算广告学
课时28 搜索广告
搜索广告的特点:1. 用户定向标签f(u):远远弱于上下文影响,一般可以忽略,但是因为搜索广告中query的信息已经很强了,用query已经足够了。2. Sesion内的短时用户搜索行为作用很重要,3. 上下文定向标签f(c):关键词。 查询词扩展 从缺点来讲,是搜索广告的运营商希望通过查询词扩展以攫取更多的利润。 做查询扩展后的广告点击的价值是要低于不做查询扩展的点击价值,但如果扩展的关键词相关的广告如果出价更高或一样高,那么对搜索广告运营商做扩展是会收入更多的。另一点从宏观上讲,通过做查询扩展,使得每一个广告主的竞价范围变大了。 方法:
- 基于推荐的方法,它是挖掘(session,query)矩阵找到相关query,session就是用户在一次查询序列中输入的查询词,可以用推荐技术中挖掘(user, item)的算法进行挖掘,这种方法利用的是搜索数据。
- 基于语义的方法,用topic model或概念化的方法中找语义相关query,对相同主题的词用topic model进行聚类,并认为它们的相似的查询意图,经过一些选择,可以将它们列到查询扩展集合中。Topic model是分析潜在语义的模型,也可以一些明确语义分析方法,它是将一些词或词组抽象成数目相对少的概念,每个概念中的词可以认为它们有相似的意图。语义分析的方法利用的是其它文档的数据。
- 基于收益的方法,这种方法在实际中效果是很好的,它不进行语义的分析,也不进行推荐分析,仅看一个查询词在历史上哪些查询词对它的eCPM变现高,但它的分析出来的数据量是很少的,一些新词和长尾的词它就无能为力了,但它是不会漏掉一些真正有经济价值的词。 用户相关的搜索广告决策
- 结果个性化对于搜索广告作用有限,前面提到过f(u)直接做audience 兴趣的targeting的意义并不大,因为上下文信息(c)太强,个人兴趣可以忽略。
- 广告展示的条数可以深度个性化,即参与position auction的位置的个数。
- 可以根据同一session内的行为调整广告结果,比如:用户在第一页没有点击任何广告,用户点击第二页时,可以不再展示第一页展示过的广告。 短时用户行为反馈 短时内用户的几次连续搜索称之为一个session,session的行为可以更明确地标定他搜索的目标。 在广告系统中,短时用户行为有两个作用,1. 短时的受众定向:根据短时行为为用户打上标签。因为短时的计算不太可能用Hadoop这样的平台进行计算,因为Hadoop平台有很长的延时,并且处理时间也不能确定。所以这个打标签的过程是与其它标签的过程是独立的。2. 短时点击反馈:根据短时广告交互计算的动态特征。 所以它可以利用流式计算(stream computing)平台,比如S4,Storm等进行计算
课时29 流式计算平台
在Storm中,一个实时应用的计算任务被打包作为Topology发布,这同Hadoop的MapReduce任务相似。流式计算是调度数据的,而Hadoop核心是调度计算
课时30 广告购买平台
广告购买平台(trading desk):链接不同媒体和广告网络,不能提供非实时的ROI广告网络Demand端。
广告购买平台(Trading Desk)
- 产品目标:Allows advertisers buy audience across publishers and ad networkds
- 关键特征: 连接到不同媒体和广告网络,为广告商提供universal marketplace
非实时竞价campaign的ROI优化能力 经常由代理公司孵化出来
-
计算广告学 笔记5.1 探索与利用
课程地址:计算广告学
课时27 探索与利用
计算广告领域的探索与利用要解决的问题是:因为长尾(a,u,c)组合极大部分在系统中并没有出现过,所以没有这些长尾(a,u,c)的统计量,所以要探索性地创造合适的展示机会以积累统计量,从而更准确地估计其CTR。但探索性的展示的过程是没有按当前的eCPM最大化方法进行广告投放,即探索的展示会让收入下降,那么如何控制探索的量和探索的有效性,使得系统长期的,整体的收入增加,就是探索与利用的核心问题。
这个问题在学术界讨论的比较多,它是Reinforcement Learning中的一个具体问题,学术界通常把它描述成为一个Multi-arm Bandit(MAB)问题。这个名字的起源来自由laohuji上的扳手,扳哪个Arm赢的概率比较大,在开始的时候是不知道的,所以要用钱去探索,看哪个扳手能提供的收益最高,但试的过程是在损失自己的钱,所以用这个名字很形象地来称这个E&E问题。
Multi-arm Bandit通常描述为:有限个arms(或称收益提供者)a(即上例中,laohuji的扳手是有限的,在广告系统中它就是广告),每个有确定有限的期望收益E(rt,a),在每个时刻t,我们必须从arms中选择一个,最终目标是优化整体收益。MAB最基本的方法学术界称为ε-greedy,它是一个很简单的方法,就是将ε比例的小部分流量用于随机探索。如果提出一种新的E&E算法,当然首先要和这种方法进行比较。
广告问题中有两个主要挑战,但它们不一定能很好地在这个框架下解决。1. 海量的组合空间需要被探索,因为要探索的是(a,u,c)这个组合空间,甚至不能认为是一个有限的空间(不是指数学上的无限),2. 因为在MAB问题中假设了各个arm的期望收益是确定的,但对于广告来讲,每个arm的收益绝对不是确定的,比如在双11促销前的ROI与其它时间的ROI相比,差的就很远了。
E&E 算法 - UCB
UCB方法的思路从直觉上非常合理,它是在时间t,通过以往观测值以及某种概率模型,计算每个arm的期望收益的upper confidence bound(UCB),并选择UCB最大的arm。先不关注这句话中的术语,它其实也是一个bayesian的理念,在估计某个arm收益的时候,不再把它认为是一个确定的数,而是把它认为是一个分布。UCB的意思是在选择的时候,并不是按照期望收益最大的一点去选择,而是按照分布的收益上界去选择。在体会这个策略的过程中,会发现它是一个很聪明的策略,它对每个arm都是选择它最有可能达到的收益点来进行投放,随着时间的推移,随着观察值的增加,分布曲线会越来越窄,最终收敛成一个固定的值。假设一个广告的期望收益并不高,换言之,它的表现可能不是最优的,我们在UCB方法下不会永远出这个广告,因为经过几次探索,它就分布曲线会迅速收敛,当发现有别的广告比它更好的时候,就不会再出这个广告了,但这种方法不会漏掉真正好的广告,因为好的广告在没有观察的时候,它是非常宽的一个函数分布,它的upper confidence是一个很大的值,所以总是有机会选中它,选中之后,分布会迅速收敛到实际的确定的收益。Paper中主要探讨的是具体的UCB策略,比如β-UCB策略,它是证明选择非最优的arms存在着一个上界,该上界与总的选择次数无关。还有一个改进的策略,UCB-tuned,它证明了如果已经选择的次数越多,就越可能自信地抛弃不太有前途(但仍可能最优)的arm。
-
计算广告学 笔记4.4 点击率预估模型
课程地址:计算广告学
课时24 点击率预测和逻辑回归
点击的概率可以很自然地用条件概率来表达,given a(广告),u(用户), c(页面),p of click。我们可以用统计来预测点击率,我个人计为Regression比Ranking的方法更合适,我们知道在搜索中,Ranking的方法被广泛地研究,利用机器学习的方法得到更好的排序结果。但我们知道广告的排序是根据eCPM,所以,广告的排序并不能仅考虑CTR,因为eCPM还要考虑Bid,换言之,对广告网络而言,竞价广告系统需要准确地估计CTR。,如果是对DSP而言,对点击率的预测要求就更高了,因为DSP需要同时估计CTR和点击价值,CTR 和点击价值决定了DSP出价,即是向Exchange报的出价。
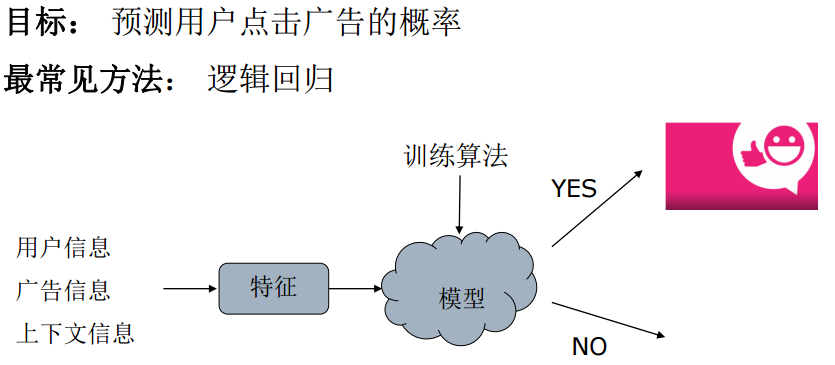
逻辑回归
Click的概率是服从Bi-nominal分布的,它的取值只能是0或1,我们很自然的想法就是用Logistic Regression模型。虽然有很多其它更Fancy的算法,但工程中常常使用的恰是这种简单的模型。 如果我们忽略二分类问题中y的取值是一个离散的取值(0或1),我们继续使用线性回归来预测y的取值。这样做会导致y的取值并不为0或1。逻辑回归使用一个函数来归一化y值,使y的取值在区间(0,1)内,这个函数称为Logistic函数(logistic function),也称为Sigmoid函数(sigmoid function)。
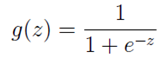
逻辑回归表达式
逻辑回归本质上是线性回归,只是在特征到结果的映射中加入了一层函数映射,即先把特征线性求和,然后使用函数g(z)将最为假设函数来预测。g(z)可以将连续值映射到0到1之间。线性回归模型的表达式带入g(z),就得到逻辑回归的表达式:
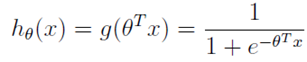
让x0 = 1,表达式就转换为:
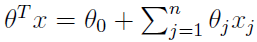
分类
现在我们将y的取值h(x)通过Logistic函数归一化到(0,1)间,y的取值有特殊的含义,它表示结果取1的概率,因此对于输入x分类结果为类别1和类别0的概率分别为:
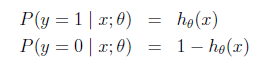
对上面的表达式合并一下就是:
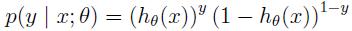
梯度上升
得到了逻辑回归的表达式,下一步跟线性回归类似,构建似然函数,然后最大似然估计,最终推导出θ的迭代更新表达式。
我们假设训练样本相互独立,那么似然函数表达式为:
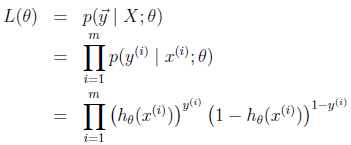
同样对似然函数取log,转换为:
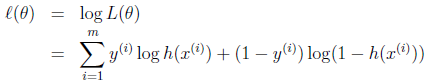
转换后的似然函数对θ求偏导,在这里我们以只有一个训练样本的情况为例:
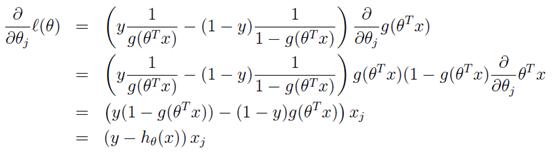
这个求偏导过程第一步是对θ偏导的转化,依据偏导公式:y=lnx y’=1/x。
第二步是根据g(z)求导的特性g’(z) = g(z)(1 - g(z)) 。
第三步就是普通的变换。
这样我们就得到了梯度上升每次迭代的更新方向,那么θ的迭代表达式为:
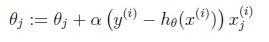
课时25 逻辑回归优化方法介绍
LGFGS:
http://www.hankcs.com/ml/l-bfgs.html
课时26 动态特征
静态特征举一个例子,上文提到过静态特征可以通过组合得到,比如年龄等于15岁并且广告是电商广告,如果user和ad满足这两个条件,则特征值为1,否则为0。而动态优化是统计出这个组合在历史上它的表现是什么情况,即年龄等于15岁且为电商广告在历史上点击率如何,历史上的点击率显示是一个特别强的指标,或者说它比1或是0代表的信息要多。动态特征即是在标签组合维度上聚合点击反馈统计作为CTR预测的特征。也可以换一个角度去理解,我们可以认为这种聚合维度上的CTR是一个弱分类器,比如上例中只知道年龄和广告类型对点击率进行预测。我们对成千上万的组合特征就可以训练得到成千上万的弱分类器,这种弱分类器再作为最后learning模型的输入特征。
动态特征的优势有:1. 工程架构扩展性比较强,因为生成动态特征,只需要在历史数据上作统一的挖掘流量,只需要进行配置就可以实现对任意特征的挖掘,它与在线学习相比,上文讲到,特征上的任何一个方案,都对应模型上的一个方案,如果在模型上快速地变weight与在特征集合上快速变特征,变特征会简单的多,因为变模型在广告投放的过程中还涉及多台机器通信的问题,变特征没有这个问题,即使你需要计算的很快速,也可以用流式计算平台实现。2. 对于新的(a, u, c)组合有较强的back-off能力,比如有一种广告素材是没有出现过的,如果想在模型中把这个特征加进去,把权重更新出来,过程是比较复杂的。如果是仅仅在特征端对它进行描述,这个素材对不同的人群的CTR都作为动态特征放在系统里,只要流式计算做的足够快,只要广告上线,就可以迅速地就可以在模型中做出正确的决策。动态特征的缺点是,因为特征都是动态的,是需要一个很大的Cache去存储,存储的量是巨大的,因为所有的组合都可以生成动态特征,另外,更新的速度要求也比较高。
-
Google Code Jam Kickstart 2017 Practice B Vote
Problem
A and B are the only two candidates competing in a certain election. We know from polls that exactly N voters support A, and exactly M voters support B. We also know that N is greater than M, so A will win.
Voters will show up at the polling place one at a time, in an order chosen uniformly at random from all possible (N + M)! orders. After each voter casts their vote, the polling place worker will update the results and note which candidate (if any) is winning so far. (If the votes are tied, neither candidate is considered to be winning.)
What is the probability that A stays in the lead the entire time – that is, that A will always be winning after every vote?
Input and Output
Input
The input starts with one line containing one integer T, which is the number of test cases. Each test case consists of one line with two integers N and M: the numbers of voters supporting A and B, respectively.
Output
For each test case, output one line containing Case #x: y, where x is the test case number (starting from 1) and y is the probability that A will always be winning after every vote.
y will be considered correct if y is within an absolute or relative error of 10-6 of the correct answer. See the FAQ for an explanation of what that means, and what formats of real numbers we accept.
Limits
1 ≤ T ≤ 100.
Small dataset
0 ≤ M < N ≤ 10.
Large dataset
0 ≤ M < N ≤ 2000.
Sample
Input
2 2 1 1 0Output
Case #1: 0.33333333 Case #2: 1.00000000In sample case #1, there are 3 voters. Two of them support A – we will call them A1 and A2 – and one of them supports B. They can come to vote in six possible orders: A1 A2 B, A2 A1 B, A1 B A2, A2 B A1, B A1 A2, B A2 A1. Only the first two of those orders guarantee that Candidate A is winning after every vote. (For example, if the order is A1 B A2, then Candidate A is winning after the first vote but tied after the second vote.) So the answer is 2/6 = 0.333333…
In sample case #2, there is only 1 voter, and that voter supports A. There is only one possible order of arrival, and A will be winning after the one and only vote.
Code
#include <iostream> #include <vector> #include <algorithm> #include <set> using namespace std; int main() { freopen("E:/B-small-practice.in","r",stdin); freopen("E:/B-small-practice.out","w",stdout); int T, N, M; cin >> T; for (int i = 0; i < T; i++) { cout << "Case #" << i + 1 << ": "; cin >> N >> M; cout << (N-M)*1.0/(N+M) << endl; } return 0; }
-
Google Code Jam Kickstart 2017 Practice A Country Leader
Problem
The Constitution of a certain country states that the leader is the person with the name containing the greatest number of different alphabet letters. (The country uses the uppercase English alphabet from A through Z.) For example, the name GOOGLE has four different alphabet letters: E, G, L, and O. The name APAC CODE JAM has eight different letters. If the country only consists of these 2 persons, APAC CODE JAM would be the leader.
If there is a tie, the person whose name comes earliest in alphabetical order is the leader.
Given a list of names of the citizens of the country, can you determine who the leader is? Input
The first line of the input gives the number of test cases, T. T test cases follow. Each test case starts with a line with an interger N, the number of people in the country. Then N lines follow. The i-th line represents the name of the i-th person. Each name contains at most 20 characters and contains at least one alphabet letter.
Input and Output
Output
For each test case, output one line containing Case #x: y, where x is the test case number (starting from 1) and y is the name of the leader.
Limits
1 ≤ T ≤ 100.
1 ≤ N ≤ 100.
Small dataset
Each name consists of at most 20 characters and only consists of the uppercase English letters A through Z.
Large dataset
Each name consists of at most 20 characters and only consists of the uppercase English letters A through Z and ‘ ‘(space).
All names start and end with alphabet letters.
Sample
Input
2 3 ADAM BOB JOHNSON 2 A AB C DEFOutput
Case #1: JOHNSON Case #2: A AB CIn sample case #1, JOHNSON contains 5 different alphabet letters(‘H’, ‘J’, ‘N’, ‘O’, ‘S’), so he is the leader.
Sample case #2 would only appear in Large data set. The name DEF contains 3 different alphabet letters, the name A AB C also contains 3 different alphabet letters. A AB C comes alphabetically earlier so he is the leader.
Code
#include <iostream> #include <vector> #include <algorithm> #include <set> using namespace std; int main() { freopen("E:/A-large-practice.in","r",stdin); freopen("E:/A-large-practice.out","w",stdout); int T, N; string s; cin >> T; for (int i = 0; i < T; i++) { cout << "Case #" << i + 1 << ": "; cin >> N; int count = 0; string res = ""; for (int j = 0; j <= N; j++) { getline(cin, s); set<char> charS; for (char c: s) if (isalpha(c)) charS.insert(c); if (charS.size() > count) { count = charS.size(); res = s; } else if (charS.size() == count) { if (s.compare(res) < 0) res = s; } } cout << res << endl; } return 0; }