Welcome to Shanshan Blog!
-
hihoCoder 1399 Shortening Sequence
Description
There is an integer array A1, A2 …AN. Each round you may choose two adjacent integers. If their sum is an odd number, the two adjacent integers can be deleted.
Can you work out the minimum length of the final array after elaborate deletions?
Input and Output
输入
The first line contains one integer N, indicating the length of the initial array.
The second line contains N integers, indicating A1, A2 …AN.
For 30% of the data:1 ≤ N ≤ 10
For 60% of the data:1 ≤ N ≤ 1000
For 100% of the data:1 ≤ N ≤ 1000000, 0 ≤ Ai ≤ 1000000000
输出
One line with an integer indicating the minimum length of the final array.
样例提示
(1,2) (3,4) (4,5) are deleted. 样例输入 7 1 1 2 3 4 4 5 样例输出 1Codes
The ideas: After multiple deletion, in the end there are only all evens or odds. So just calculate the number differences between the evens and the odds.
#include <iostream> using namespace std; int main() { int count = 0; int n, a; cin >> n; while (n--) { cin >> a; if (a%2 ==0) count++; else count--; } cout << (count>0?count:-count) << endl; return 0; }
-
DirectX Tutroial 3 Transform Vertices
- Description
- World Transformation
- View Transformation
- Projection Transformation
- Setting the World Transformation
- Setting the View Transformation
- Setting the Projection Transformation
This tutorials are based on the DirectX Tutorial, show how to transform vertices, or convert them from 3D coordinates to screen coordinates using DirectX 9.
Description
let’s take a look at everything that happens to translate something from 3D coordinates to a flat image. There is a sequence of actions which must occur before an object appears on the screen properly. This sequence of actions is known as the Geometry Pipeline. It is called a pipeline because vertices are put through each step one at a time, and at each step along the “pipe”, the vertex is rendered into its flat image form.

Before we go to the details, let me explain the three transforms in a very easy way. When we are going to take a pictures, there are four steps:
put the staff you are going to photo in the position (world transformation)
modify the camera angle (view transformation)
modify the focal distance (project transformation) take a pictureWorld Transformation
Changes coordinates from model space to world space. In other words, it places a model in a world at an exact point defined by coordinates.
Of course, being able to move an object into world space is always useful, but it can get rather limiting if your model is always facing the same direction. A spaceship that can only face East is rather dull and does not elicit much thrill or adrenaline (or so I find).
And so another part of World Transformation is rotation. Rotation is the process of spinning 3D objects along an axis.
Another important part of World Transformation is scaling. Scaling is the action of making a 3D object larger or smaller.
View Transformation
View transformation is a process which sets up the 3D coordinate system to point in the proper direction. What this means is that the directions of each axis are going to change to point in different directions.
Direct3D uses the concept of a virtual camera. This camera has an exact position and points at an exact vector. When world transformation is done, the 3D axes have no alignment to how the scene will be viewed.
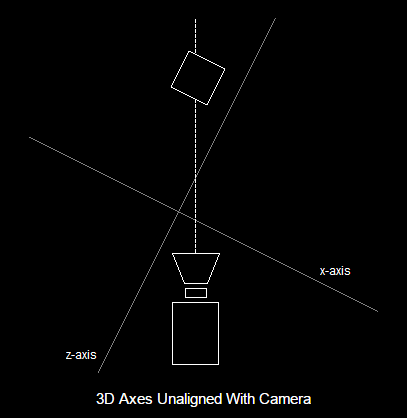
In order for Direct3D and the video card to quickly process the 3D scene, the 3D axes must align with the camera. Specifically, the origin is repositioned to where the camera is, and the z-axis points directly down the line of sight.
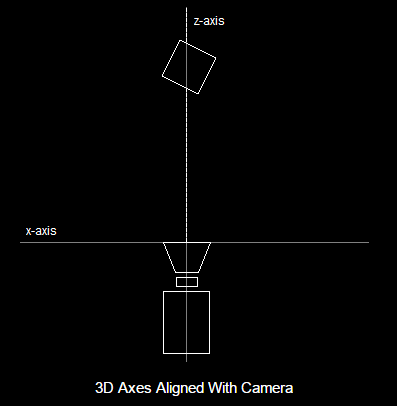
Projection Transformation
If view transformation can be thought of as a camera, then this step can be thought of as a lens. Once view transformation is completed, we have to change the 3D scene into one big 2D image so it can be drawn on the screen. The process that does this is called projection transformation. It is simply the converting of 3D coordinates to screen coordinates.
Let’s see how to do them in DirectX3D.
Setting the World Transformation
Transformation
D3DXMATRIX matTranslate; // a matrix to store the translation information // build a matrix to move the model 12 units along the x-axis and 4 units along the y-axis // store it to matTranslate D3DXMatrixTranslation(&matTranslate, 12.0f, 4.0f, 0.0f); // tell Direct3D about our matrix d3ddev->SetTransform(D3DTS_WORLD, &matTranslate);Rotation
D3DXMATRIX matRotateX; // a matrix to store the rotation information // build a matrix to rotate the model 3.14 radians D3DXMatrixRotationX(&matRotateX, 3.14f); // tell Direct3D about our matrix d3ddev->SetTransform(D3DTS_WORLD, &matRotateX);Scaling
D3DXMATRIX matScale; // a matrix to store the scaling information // build a matrix to double the size of the model // store it to matScale D3DXMatrixScaling(&matScale, 2.0f, 2.0f, 2.0f); // tell Direct3D about our matrix d3ddev->SetTransform(D3DTS_WORLD, &matScale);If you want to combine all of them, you can just do this:
d3ddev->SetTransform(D3DTS_WORLD, &(matTranslate * matRotateX * matRotateY * matRotateZ * matScale));Setting the View Transformation
Setting the view transformation can be considered to be similar to setting up a virtual camera. All a programmer does with this is feed the camera position, direction and rotation into a single matrix.
D3DXMATRIX matView; // the view transform matrix D3DXMatrixLookAtLH(&matView, &D3DXVECTOR3 (100.0f, 100.0f, 100.0f), // the camera position &D3DXVECTOR3 (0.0f, 0.0f, 0.0f), // the look-at position &D3DXVECTOR3 (0.0f, 1.0f, 0.0f)); // the up direction d3ddev->SetTransform(D3DTS_VIEW, &matView); // set the view transform to matViewSetting the Projection Transformation
If view transformation can be considered the camera setup, then projection transformation can be thought of as the camera lens. It is probably the most complex type of transformation. It is simple in code (as it only needs one matrix, set by a single function), but it has a lot of factors which control it.
D3DXMATRIX matProjection; // the projection transform matrix D3DXMatrixPerspectiveFovLH(&matProjection, D3DXToRadian(45), // the horizontal field of view (FLOAT)SCREEN_WIDTH / (FLOAT)SCREEN_HEIGHT, // aspect ratio 1.0f, // the near view-plane 100.0f); // the far view-plane d3ddev->SetTransform(D3DTS_PROJECTION, &matProjection); // set the projection transformWe don’t have any code to add lights just yet, and without these, nothing will appear at all. Let’s change that by turning off the lights just for now, and having everything show up normally (as if everything were lit automatically).
d3ddev->SetRenderState(D3DRS_LIGHTING, FALSE); // turn off the 3D lightingsYou can get the complete codes from Github
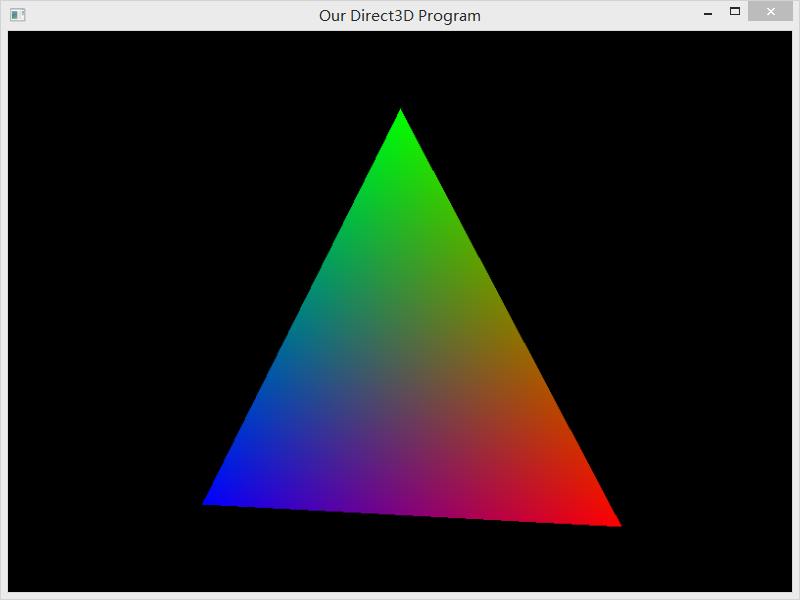
If you run this program you should get something like this:
-
hihoCoder 1288 Font Size
Description
Steven loves reading book on his phone. The book he reads now consists of N paragraphs and the i-th paragraph contains ai characters.
Steven wants to make the characters easier to read, so he decides to increase the font size of characters. But the size of Steven’s phone screen is limited. Its width is W and height is H. As a result, if the font size of characters is S then it can only show ⌊W / S⌋ characters in a line and ⌊H / S⌋ lines in a page. (⌊x⌋ is the largest integer no more than x)
So here’s the question, if Steven wants to control the number of pages no more than P, what’s the maximum font size he can set? Note that paragraphs must start in a new line and there is no empty line between paragraphs.
Input and Output
输入
Input may contain multiple test cases.
The first line is an integer TASKS, representing the number of test cases.
For each test case, the first line contains four integers N, P, W and H, as described above.
The second line contains N integers a1, a2, … aN, indicating the number of characters in each paragraph.
For all test cases,
1 <= N <= 103,
1 <= W, H, ai <= 103,
1 <= P <= 106,
There is always a way to control the number of pages no more than P.
输出
For each testcase, output a line with an integer Ans, indicating the maximum font size Steven can set.
样例输入 2 1 10 4 3 10 2 10 4 3 10 10 样例输出 3 2Codes
#include <iostream> #include <math.h> using namespace std; int main() { int m, N, P, W, H; int a[1005]; cin >> m; while (m--) { cin >> N >> P >> W >> H; for (int i=0; i<N; i++) cin >> a[i]; int max = W>H?H:W; for (int i=max; ;i--) { int lines = 0; int perline = W/i; for (int j=0; j<N; j++) lines += ceil(a[j]/(double)perline); if (ceil(lines/(H/i)) <=P) { cout << i << endl; break; } } } return 0; }
-
hihoCoder 1051 补提交卡
Description
小Ho给自己定了一个宏伟的目标:连续100天每天坚持在hihoCoder上提交一个程序。100天过去了,小Ho查看自己的提交记录发现有N天因为贪玩忘记提交了。于是小Ho软磨硬泡、强忍着小Hi鄙视的眼神从小Hi那里要来M张”补提交卡”。每张”补提交卡”都可以补回一天的提交,将原本没有提交程序的一天变成有提交程序的一天。小Ho想知道通过利用这M张补提交卡,可以使自己的”最长连续提交天数”最多变成多少天。
Input and Output
输入
第一行是一个整数T(1 <= T <= 10),代表测试数据的组数。
每个测试数据第一行是2个整数N和M(0 <= N, M <= 100)。第二行包含N个整数a1, a2, … aN(1 <= a1 < a2 < … < aN <= 100),表示第a1, a2, … aN天小Ho没有提交程序。
输出
对于每组数据,输出通过使用补提交卡小Ho的最长连续提交天数最多变成多少。
样例输入 3 5 1 34 77 82 83 84 5 2 10 30 55 56 90 5 10 10 30 55 56 90 样例输出 76 59 100Codes
#include <iostream> #include <string> using namespace std; int data[105]; int main() { int T; scanf("%d", &T); int n, m; while (T--) { scanf("%d%d", &n, &m); for (int i=1; i<=n; i++) scanf("%d%", &data[i]); if (m>=n) cout << 100 << endl; else { int res = 0; for (int i=m+1; i<=n; i++) { if (data[i] - data[i-m-1] - 1 > res) res = data[i] - data[i-m-1] - 1; } cout << res << endl; } } return 0; }
-
hihoCoder 1040 矩形判断
Description
给出平面上4条线段,判断这4条线段是否恰好围成一个面积大于0的矩形。
Input and Output
输入
输入第一行是一个整数T(1<=T<=100),代表测试数据的数量。
每组数据包含4行,每行包含4个整数x1, y1, x2, y2 (0 <= x1, y1, x2, y2 <= 100000);其中(x1, y1), (x2,y2)代表一条线段的两个端点。
输出
每组数据输出一行YES或者NO,表示输入的4条线段是否恰好围成矩形。
样例输入 3 0 0 0 1 1 0 1 1 0 1 1 1 1 0 0 0 0 1 2 3 1 0 3 2 3 2 2 3 1 0 0 1 0 1 1 0 1 0 2 0 2 0 1 1 1 1 0 1 样例输出 YES YES NOCodes
#include <iostream> #include <set> using namespace std; struct point { int x, y; bool operator<(const point& p2)const { //优先判断横坐标 if(x<p2.x||(x==p2.x&&y<p2.y)) return true; return false; } bool operator==(const point& p2) const { return (x==p2.x&&y==p2.y); } }; struct line { point p1; point p2; }; bool fourPoints(line lines[4]) { set<point> s; for (int i=0; i<4; i++) { s.insert(lines[i].p1); s.insert(lines[i].p2); } return s.size()==4; } bool isValid(line lines[4]) { for (int i=1; i<4; i++) { if ((lines[i].p1.x-lines[i].p2.x)*(lines[0].p1.x-lines[0].p2.x) == (lines[i].p1.y-lines[i].p2.y)*(lines[0].p1.y-lines[0].p2.y)) continue; if ((lines[i].p1.x-lines[i].p2.x)*(lines[0].p2.y-lines[0].p1.y) == (lines[0].p1.x-lines[0].p2.x)*(lines[i].p1.y-lines[i].p2.y)) continue; return false; } return true; } int main() { int n; cin >> n; line lines[4]; while (n--) { for (int i=0; i<4; i++) { cin >> lines[i].p1.x >> lines[i].p1.y >> lines[i].p2.x >> lines[i].p2.y; } if (!fourPoints(lines)) cout << "NO" << endl; else { if (!isValid(lines)) cout << "NO" << endl; else cout << "YES" << endl; } } return 0; }
-
DirectX Tutroial 2 Vertext to Draw a Triangle
This tutorials are based on the DirectX Tutorial, show how to create a triangle using DirectX 9.
Set up the global variable
LPDIRECT3D9 g_pD3D = NULL; // Used to create the D3DDevice LPDIRECT3DDEVICE9 g_pd3dDevice = NULL; // Our rendering device LPDIRECT3DVERTEXBUFFER9 g_pVB = NULL; // Buffer to hold verticescreate a structure as the vertex, here we include the location and the diffuse color.
Now we need to create the vertices using our new format. We do it by building a simple struct containing the variables we included in the FVF code.
#define CUSTOMFVF (D3DFVF_XYZRHW | D3DFVF_DIFFUSE) struct CUSTOMVERTEX { FLOAT x, y, z, rhw; // from the D3DFVF_XYZRHW flag DWORD color; // from the D3DFVF_DIFFUSE flag }Use the structure to create the triangle
CUSTOMVERTEX OurVertices[] = { {320.0f, 50.0f, 1.0f, 1.0f, D3DCOLOR_XRGB(0, 0, 255),}, {520.0f, 400.0f, 1.0f, 1.0f, D3DCOLOR_XRGB(0, 255, 0),}, {120.0f, 400.0f, 1.0f, 1.0f, D3DCOLOR_XRGB(255, 0, 0),}, };Now we need to get the triangle ready for DirectX3D to use. To do this, we create what is called a vertex buffer. A vertex buffer is simply an interface that stores a section in memory (either Video RAM or system memory) to holds information about the vertices/models in your game.
// Create the vertex buffer. Here we are allocating enough memory // (from the default pool) to hold all our 3 custom vertices. We also // specify the FVF, so the vertex buffer knows what data it contains. if (FAILED(g_pd3dDevice->CreateVertexBuffer(3 * sizeof(CUSTOMVERTEX), 0, D3DFVF_CUSTOMVERTEX, D3DPOOL_DEFAULT, &g_pVB, NULL))) { return E_FAIL; }Now we fill the vertex buffer. To do this, we need to Lock() the VB to gain access to the vertices. This mechanism is required becuase vertex buffers may be in device memory.
VOID* pVertices; if (FAILED(g_pVB->Lock(0, sizeof(vertices), (void**)&pVertices, 0))) return E_FAIL; // to copy the vertices to the vertex buffer memcpy(pVertices, vertices, sizeof(vertices)); g_pVB->Unlock();Then drawing the primitive
VOID Render() { // Clear the backbuffer to a blue color g_pd3dDevice->Clear( 0, NULL, D3DCLEAR_TARGET, D3DCOLOR_XRGB( 0, 0, 255 ), 1.0f, 0 ); // Begin the scene if( SUCCEEDED( g_pd3dDevice->BeginScene() ) ) { // tells Direct3D which vertex buffer we are drawing from g_pd3dDevice->SetStreamSource( 0, g_pVB, 0, sizeof( CUSTOMVERTEX ) ); // tells Direct3D what FVF code we are using currently g_pd3dDevice->SetFVF( D3DFVF_CUSTOMVERTEX ); // do the actual rendering g_pd3dDevice->DrawPrimitive( D3DPT_TRIANGLELIST, 0, 1 ); // End the scene g_pd3dDevice->EndScene(); } // Present the backbuffer contents to the display g_pd3dDevice->Present( NULL, NULL, NULL, NULL ); }You can get the complete codes from Github
If you run this program you should get something like this: