Leetcode Rectangle
Leetcode 84. Largest Rectangle in Histogram
Given n non-negative integers representing the histogram’s bar height where the width of each bar is 1, find the area of largest rectangle in the histogram.
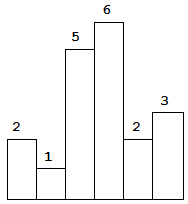
Above is a histogram where width of each bar is 1, given height = [2,1,5,6,2,3].
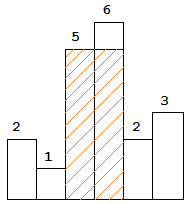
The largest rectangle is shown in the shaded area, which has area = 10 unit.
For example,
Given heights = [2,1,5,6,2,3],
return 10.
class Solution {
public:
int largestRectangleArea(vector<int>& heights) {
int res = 0;
heights.push_back(0);
vector<int> index;
for (int i = 0; i < heights.size(); i++) {
while (index.size() > 0 && heights[index.back()] >= heights[i]) {
int h = heights[index.back()];
index.pop_back();
int idx = index.size() > 0 ? index.back():-1;
if (h * (i-idx-1) > res)
res = h * (i-idx-1);
}
index.push_back(i);
}
return res;
}
};
Leetcode 85. Maximal Rectangle
Given a 2D binary matrix filled with 0’s and 1’s, find the largest rectangle containing only 1’s and return its area.
For example, given the following matrix:
1 0 1 0 0
1 0 1 1 1
1 1 1 1 1
1 0 0 1 0
Return 6.
class Solution {
public:
int maximalRectangle(vector<vector<char>>& matrix) {
if (matrix.size() == 0 || matrix[0].size() == 0) return 0;
int m = matrix.size(), n = matrix[0].size(), res = 0;
vector<int> left(n, 0), right(n, n), height(n, 0);
for (int i = 0; i < m; i++) {
int cur_left = 0, cur_right = n;
for (int j = 0; j < n; j++)
height[j] = matrix[i][j] == '1' ? height[j]+1 : 0;
for (int j = 0; j < n; j++) {
left[j] = matrix[i][j] == '1' ? max(left[j], cur_left) : 0;
cur_left = matrix[i][j] == '1' ? cur_left : j+1;
}
for (int j = n-1; j >= 0; j--) {
right[j] = matrix[i][j] == '1' ? min(right[j], cur_right) : n;
cur_right = matrix[i][j] == '1' ? cur_right : j;
}
for (int j = 0; j < n; j++)
res = max(res, (right[j]- left[j])*height[j]);
}
return res;
}
};