课程地址:计算广告学
课时10 常用广告系统开源工具
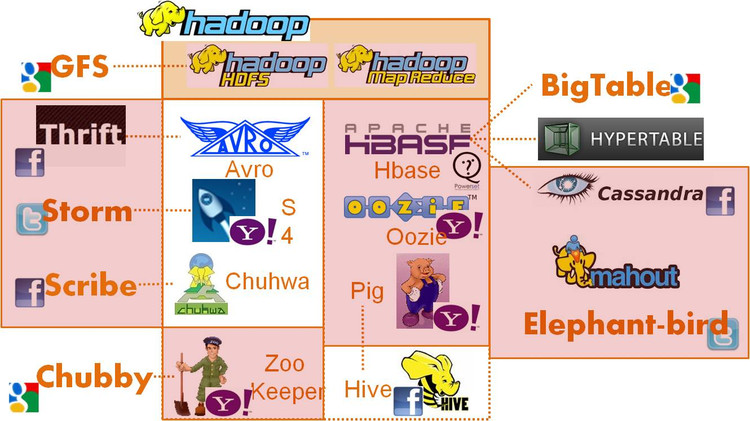
-
离线数据处理: hadoop/hbase/cassandra
-
在线数据处理:storm/s4
-
跨语言通信:thrift/proobuf/avro, elephant bird
-
一致性:zoo keeper/chubby
-
数据查看:hive/pig
-
数据传输:scribe
课时11 合约广告简介
在线广告的方法有:
- 担保式投送(Guaranteed Delivery, GD)
基于合约的广告机智,约定的量未完成需要向广告商补偿 量(Quantity)优先于质(Quality)的销售方式 多采用千次展示付费(Cose per Mille, CPM)方式结算
- 广告投放机(Ad server)
CPM方式必然要求广告投送由服务器端完成决策 受众定向,CTR预测和流量预测是广告投放机的基础 GD合约下,投放机满足各合约的量,并尽可能优化各广告主流量的质
竞价广告(CPM/CPC/CPA):竞价广告,即根据实时竞价,在信息流中以不固定位置出现,并按照广告效果付费的广告形式。竞价期间,出价较高的广告主可获得优先展示资格,其广告效果同时可获得更多保证。
-
CPM(cost per mille):千人展示成本,即广告被展示1000次所需要的费用。
-
CPC(cost per click):单次点击成本,即广告被点击一次所需要的费用。
-
CPA(cost per action):单次下载成本,即APP被下载一次所需要的费用。仅限安卓APP。
课时12 在线分配问题
在线分配问题的核心是:在量的某种类型的限制下,完成对质的优化。
因为有量的限制,它是一个constrained optimization(受限优化)的问题,最早google提出的是AdWords Problem。
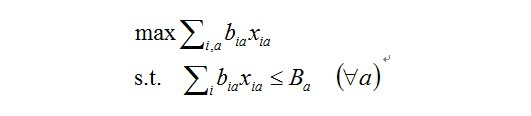
目标函数,b_ia是把一次展示(Impression,i)分给一个(Ad, a)产生的收益(bid * ctr, b,即ecpm),xia是指一次展示(impression, i)是否分给了一个广告(Ad, a),这个值只能为0或是1,因为一次展示只能或是分配给一个广告,或是没分配。sum(i, a)也就是整个系统的收益,max sum(i,a)即是优化的核心问题:如何最大化整个系统的收益。它的限制是:对每个广告商来讲,有一个budget,每个广告商所消耗的资金应该小于他的budget,即式中Ba。
后来研究者把这个问题推广到display problem,display problem中有很多CPM的campaign,它希望优化的是每一个CPM的效果。
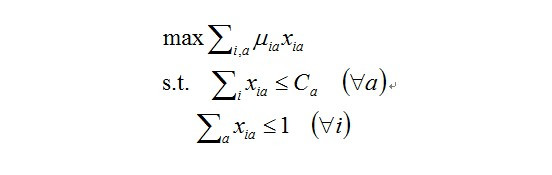
效果即是它收获到的点击量,点击量的计算方法为把所有的展示的Xia乘上点击率起来就是点击量。优化目标有两个constrain,一个是称之为Demand Constrain,它是指每一个广告商来讲,他需要Ca次展示,那么媒体提供的展示数应该小于等于Ca,注意这里是NGD的问题,广告系统提供的展示次数可以小于需求的量,另一个Constrain是Supply Constrain,是对于任何展示,xia加起来小于等于1,可以小于是因为这次广告也可以不分配给任何广告,它可以交给下游的其它变现手段。
拉格朗日方法
http://blog.csdn.net/wangkr111/article/details/21170809
这里引入了对偶函数,原因是因为包含了不等式约束的极值问题.探讨有不等式约束的极值问题求法,问题如下:
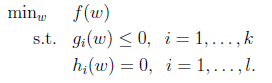
我们定义一般化的拉格朗日公式
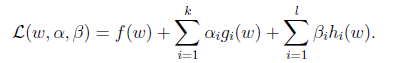
这里的alpha和beta都是拉格朗日算子。如果按这个公式求解,会出现问题,因为我们求解的是最小值,而这里的g(w)已经不是0了,我们可以将alpha调整成很大的正值,来使最后的函数结果是负无穷。因此我们需要排除这种情况,我们定义下面的函数:
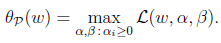
这里的P代表primal。那么我们总是可以调整alpha和beta来theta使得有最大值为正无穷。而只有g和h满足约束时,为f(w)。这个函数的精妙之处在于a_i>0,而且求极大值。 因此我们可以写作
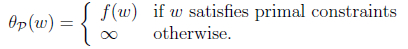
怎么求解? 我们先考虑另外一个问题
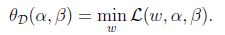
D的意思是对偶,将问题转化为先求拉格朗日关于w的最小值,将alpha和β看作是固定值。之后在求最大值的话:
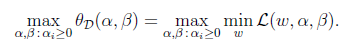
High Water Mark算法
Yahoo!实际系统中用的方法,它分两个阶段,离线计划阶段和在线分配阶段。

课程13 Hadoop简介
Hadoop目标可以概括为:可扩展性: Petabytes (1015 Bytes) 级别的数据量, 数千个节点,经济性: 利用商品级(commodity)硬件完成海量数据存储和计算,可靠性: 在大规模集群上提供应用级别的可靠性。
Hadoop包含两个部分:
- HDFS
HDFS即Hadoop Distributed File System(Hadoop分布式文件系统),HDFS具有高容错性,并且可以被部署在低价的硬件设备之上。HDFS很适合那些有大数据集的应用,并且提供了对数据读写的高吞吐率。HDFS是一个master/slave的结构,就通常的部署来说,在master上只运行一个Namenode,而在每一个slave上运行一个Datanode。
- MapReduce
Map/Reduce模型中Map之间是相互独立的,因为相互独立,使得系统的可靠性大大提高了。
它是用调度计算代替调度,在处理数据时,是将程序复制到目标机器上,而不是拷贝数据到目标计算机器上。
常用的统计模型
机器学习的算法有很多分类,其中有统计机器学习算法,统计机器学习在Hadoop上仅仅实现其逻辑是比较简单的。常用的统计模型可以大致归为下面两个类别:
- 指数族分布
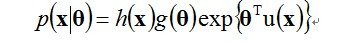
指数族分布是由最大熵的原则推导出来的,即在最大熵的假设下,满足一定条件的分布可以证明出是指数族的分布。指数族分布函数包括:Gaussian multinomial, maximum entroy。
指数族分布在工程中大量使用是因为它有一个比较好的性质,这个性质可以批核为最大似然(Maximum likelihook, ML)估计可以通过充分统计量(sufficient statistics)链接到数据(注:摘自《Pattern Recognition》),要解模型的参数,即对theta做最大似然估计,实际上可以用充分统计量来解最大似然估计:
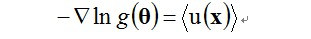
充分估计量大小是与模型的参数的空间复杂度成正比,和数据没有关系。换言之,在你的数据上计算出充分统计量后,最就可以将数据丢弃了,只用充分统计量。比如求高斯分布的均值和方差,只需要求出样本的与样本平方和。
Map Reduce 统计学习模型
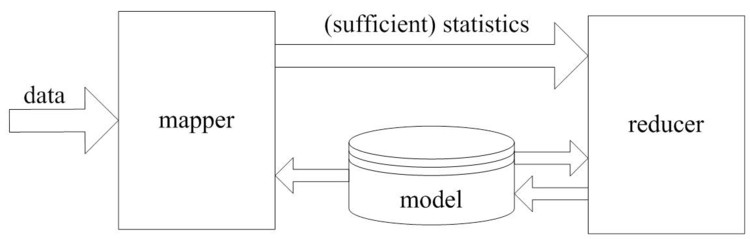
Map的过程是收集充分统计量,充分统计量的形式是u(x),它是指数族函数变换函数的均值。所以我们只需要得到u(x)的累加值,对高斯分布来讲,即得到样本之和,和样本平方和。Reduce即根据最大似然公式解出theta。即在在mapper中仅仅生成比较紧凑的统计量, 其大小正比于模型参数量, 与数据量无关。在图中还有一个反馈的过程,是因为是EM算法,EM是模拟指数族分布解的过程,它本质上还是用u(x)解模型中的参数,但它不是充分统计量所以它解完之后还要把参数再带回去,进行迭代。