Leetcode N-Queen I, II
Leetcode 51. N-Queens
The n-queens puzzle is the problem of placing n queens on an n×n chessboard such that no two queens attack each other.
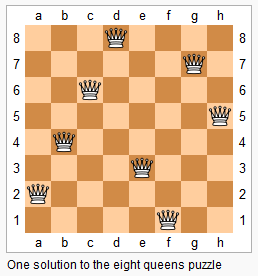
Given an integer n, return all distinct solutions to the n-queens puzzle.
Each solution contains a distinct board configuration of the n-queens’ placement, where ‘Q’ and ‘.’ both indicate a queen and an empty space respectively.
For example, There exist two distinct solutions to the 4-queens puzzle:
` [ [“.Q..”, // Solution 1 “…Q”, “Q…”, “..Q.”],
[”..Q.”, // Solution 2 “Q…”, “…Q”, “.Q..”] ] `
class Solution {
public:
void helper(int row, int col, int dia, int back_dia, vector<vector<string>> &res, vector<string> &board, int n) {
if (row==n) {
res.push_back(board);
return;
}
for (int i=0; i<n; i++) {
int curr = 1<<i;
if (curr&col || curr&back_dia || curr&dia) continue;
board[row][i] = 'Q';
helper(row+1, col|curr, (dia|curr)>>1, (back_dia|curr)<<1, res, board, n);
board[row][i] = '.';
}
}
vector<vector<string>> solveNQueens(int n) {
string dots(n, '.');
vector<string> board(n, dots);
vector<vector<string>> res;
helper(0, 0, 0, 0, res, board, n);
return res;
}
};
Leetcode 52. N-Queens II
Follow up for N-Queens problem.
Now, instead outputting board configurations, return the total number of distinct solutions.
class Solution {
public:
void helper(int row, int col, int dia, int back_dia, int n, int &count) {
if (row==n) {
count++;
return;
}
for (int i=0; i<n; i++) {
int curr = 1<<i;
if (curr&col || curr&back_dia || curr&dia) continue;
helper(row+1, col|curr, (dia|curr)>>1, (back_dia|curr)<<1, n, count);
}
}
int totalNQueens(int n) {
int count = 0;
helper(0, 0, 0, 0, n, count);
return count;
}
};