Cross validation is a model evaluation method that is better than residuals. The problem with residual evaluations is that they do not give an indication of how well the learner will do when it is asked to make new predictions for data it has not already seen. One way to overcome this problem is to not use the entire data set when training a learner. Some of the data is removed before training begins. Then when training is done, the data that was removed can be used to test the performance of the learned model on new data. This is the basic idea for a whole class of model evaluation methods called cross validation.
Data and model preparation:
import numpy as np
from sklearn.model_selection import train_test_split
from sklearn import datasets
from sklearn import svm
iris = datasets.load_iris()
X_train, X_test, y_train, y_test = train_test_split(iris.data, iris.target, test_size=0.4, random_state=0)
clf = svm.SVC(kernel='linear', C= 1).fit(X_train, y_train)
- Hold-Out Method
The holdout method is the simplest kind of cross validation. The data set is separated into two sets, called the training set and the testing set. The function approximator fits a function using the training set only. Then the function approximator is asked to predict the output values for the data in the testing set. The errors it makes are accumulated as before to give the mean absolute test set error, which is used to evaluate the model. The advantage of this method is that it is usually preferable to the residual method and takes no longer to compute. However, its evaluation can have a high variance.
- K-fold cross validation
K-fold cross validation is one way to improve over the holdout method. The data set is divided into k subsets, and the holdout method is repeated k times. Each time, one of the k subsets is used as the test set and the other k-1 subsets are put together to form a training set. Then the average error across all k trials is computed. The advantage of this method is that it matters less how the data gets divided. Every data point gets to be in a test set exactly once, and gets to be in a training set k-1 times. The variance of the resulting estimate is reduced as k is increased. The disadvantage of this method is that the training algorithm has to be rerun from scratch k times, which means it takes k times as much computation to make an evaluation.
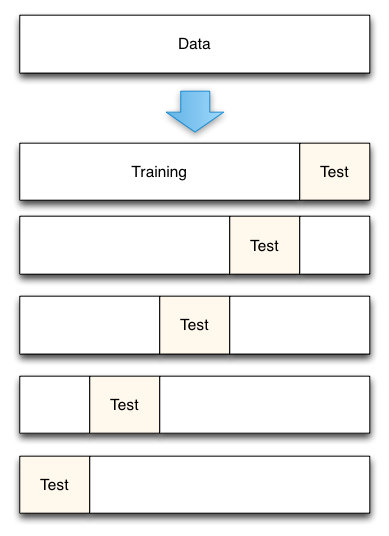
# k-folder cross validation
scores = cross_val_score(clf, iris.data, iris.target, cv=5)
print scores
The output is:
[ 0.96666667 1. 0.96666667 0.96666667 1. ]
Accuracy: 0.98 (+/- 0.03)
- Cross validation iterators
K Folder
KFold divides all the samples in k groups of samples, called folds (if k = n, this is equivalent to the Leave One Out strategy), of equal sizes (if possible). The prediction function is learned using k - 1 folds, and the fold left out is used for test.
# k folder
X = ["a", "b", "c", "d"]
from sklearn.model_selection import KFold
kf = KFold(n_splits=2)
for train, test in kf.split(X):
print ("%s %s" % (train, test))
# Each fold is constituted by two arrays: the first one is related to the training set, and the second one to the test set.
X = np.array([[0., 0.], [1., 1.], [-1., -1.], [2., 2.]])
y = np.array([0, 1, 0, 1])
X_train, X_test, y_train, y_test = X[train], X[test], y[train], y[test]
print X_train
Leave One Out
Each learning set is created by taking all the samples except one, the test set being the sample left out. Thus, for n samples, we have n different training sets and n different tests set. This cross-validation procedure does not waste much data as only one sample is removed from the training set:
# leave out
from sklearn.model_selection import LeavePOut
X = np.ones(4)
lpo = LeavePOut(p = 2)
for train, test in lpo.split(X):
print("%s %s" % (train, test))