KNN Review

• What is KNN (K-Nearest Neighbors Algorithm)
• How to Compute KNN Algorithm
• Distance Calculation
• How to Choose K (Neighbors)
• Weight
• Algorithm
• Improvement Summary
• Reference

KNN Review

What is KNN (K-Nearest Neighbors Algorithm)

K Nearest Neighbor is one of classification algorithms that are very simple to understand but works incredibly well in practice. In pattern recognition, the k-Nearest Neighbors algorithm is a non-parametric method used for classification and regression [1]. In both cases, the input consists of the k closest training examples in the feature space. 

When a prediction is required for a unseen data instance, the KNN algorithm will search through the training dataset for the k-most similar instances. The prediction attribute of the most similar instances is summarized and returned as the prediction for the unseen instance.

Take a simple example to describe it:

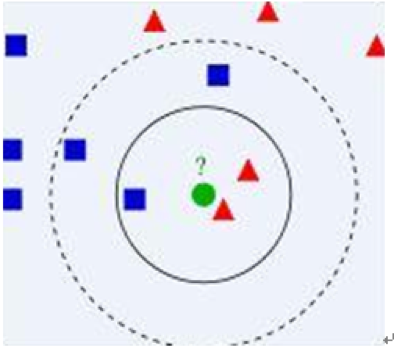
In Figure 1, there are two type data, including blue diamond and red triangle. Assume that our task is to find which class the green data belong to. How do we do it? Assume that only the nearest ones are helpful to find its classification. But how many objects to determine it? If k = 3 (solid line circle) it is assigned to the second class because there are 2 triangles and only 1 square inside the inner circle. If k = 5 (dashed line circle) it is assigned to the first class (3 squares vs. 2 triangles inside the outer circle).

How to Compute KNN Algorithm

Step 1: Calculate the distances between the current node and the nodes in the dataset

Step 2: Sort all the distances

Step 3: Choose the minimum K distance

Step 4: Return the classification with the highest frequency

Distance Calculation

Often, the classification accuracy of KNN can be improved significantly if the distance metric is learned with specialized algorithms such as Large Margin Nearest Neighbor [2] or Neighborhood components analysis [3]. Euclidean metric is the most popular choice for the distance function. If the measurement variables are not of comparable units and scales, it is more meaningful to standardize the variables before using the Euclidean distance for classification.

If an estimate of the pooled dispersion matrix is used for standardization, it essentially leads to classification using Mahalanobis distances [12]. And many other flexible metrics can be used as well [15, 16].

How to Choose K (Neighbors)

Performance of a nearest neighbor classifier depends on the distance function and the value of the neighborhood parameter k. The neighborhood parameter k, which controls the volume of the neighborhood and consequently the smoothness of the density estimates, plays an important role on the performance of a nearest neighbor classifier.

Existing theoretical results [8, 1] suggest that if Euclidean distance is used for classification, one should vary k with n in such a way that and as . The same assertion holds also for Mahalanobis distance if one uses any consistent estimate of the pooled dispersion matrix for standardization. However, for small or moderately large sample sizes, there is no theoretical guideline for choosing the optimum value of k. This optimum value depends on the specific data set and it is to be estimated using the available training sample observations.

In practice, one uses cross-validation methods [9, 10] to estimate the misclassification rate for different values of k and chooses that one which leads to the lowest estimate of misclassification rate. However, these cross-validation techniques use naive empirical proportions for estimating the misclassification probabilities. As a consequence, multiple values of k as minimizers of estimated misclassification rate, is difficult to choose the optimum one. Ghosh and Chaudhuri [11] proposed a smooth estimate for the misclassification probability function for finding the optimal bandwidth parameter.

Weight

Usually, uniform weights are used in K-Nearest Neighbor Algorithm. In other words, all points in each neighborhood are weighted equally. It takes the assumption that training data are evenly distributed among all categories. However, there is no guarantee that training set is balanced populated.

As an improvement to KNN, distance-weighted KNN method was introduced that closer neighbors of a query point will have a greater influence than neighbors which are further away. Dudani introduced a distance-weighted KNN rule (WKNN) with the basic idea of weighting close neighbors more heavily, according to their distances to the query [4]. Songbo Tan proposed Neighbor-Weighted K-Nearest Neighbor (NWKNN) for unbalanced text categorization problems. NWKNN assigns a big weight for neighbors from small class, and assigns a little weight for neighbors contained in large category [5].

Another popular framework is Voting method [6], which combines the predictions of multiple same classifiers to boost classification accuracy. Voting algorithms can be divided into two types: Bagging and Boosting. The main difference between the two types is the way the different versions of the training set are created. Bagging use a uniform probability to select a new training set while Boosting according to how often one example was misclassified by previous classifiers to select one example to create a new training set [7].

Algorithm

Advanced Improvement

Improvement Summary

Test Data: Iris Plants Database (From Python Package) Base data: [‘sepal length (cm)’, ‘sepal width (cm)’, ‘petal length (cm)’, ‘petal width (cm)’] – Four Features Target: [‘setosa’, ‘versicolor’, ‘virginica’] – Three Type Iris Plants Number of Instances: 150 (50 in each of three classes)

Reference

[1] Cover T, Hart P. Nearest neighbor pattern classification[J]. IEEE transactions on information theory, 1967, 13(1): 21-27.

[2] Weinberger K Q, Blitzer J, Saul L K. Distance metric learning for large margin nearest neighbor classification[C]//Advances in neural information processing systems. 2005: 1473-1480.

[3] Goldberger J, Hinton G E, Roweis S T, et al. Neighbourhood components analysis[C]//Advances in neural information processing systems. 2004: 513-520.

[4] Dudani S A. The distance-weighted k-nearest-neighbor rule[J]. IEEE Transactions on Systems, Man, and Cybernetics, 1976 (4): 325-327.

[5] Tan S. Neighbor-weighted k-nearest neighbor for unbalanced text corpus[J]. Expert Systems with Applications, 2005, 28(4): 667-671.

[6] Sebastiani F. Machine learning in automated text categorization[J]. ACM computing surveys (CSUR), 2002, 34(1): 1-47.

[7] Tan S. An effective refinement strategy for KNN text classifier[J]. Expert Systems with Applications, 2006, 30(2): 290-298.

[8] Loftsgaarden D O, Quesenberry C P. A nonparametric estimate of a multivariate density function[J]. The Annals of Mathematical Statistics, 1965, 36(3): 1049-1051.

[9] Lachenbruch P A, Mickey M R. Estimation of error rates in discriminant analysis[J]. Technometrics, 1968, 10(1): 1-11.

[10] Stone M. Cross-validation: a review 2[J]. Statistics: A Journal of Theoretical and Applied Statistics, 1978, 9(1): 127-139.

[11] Ghosh A K, Chaudhuri P. Optimal smoothing in kernel discriminant analysis[J]. Statistica Sinica, 2004: 457-483.

[12] Mahalanobis P C. On the generalized distance in statistics[J]. Proceedings of the National Institute of Sciences (Calcutta), 1936, 2: 49-55.

[13] Friedman J H. Flexible metric nearest neighbor classification[R]. Technical report, Department of Statistics, Stanford University, 1994.

[14] Hastie T, Tibshirani R. Discriminant adaptive nearest neighbor classification[J]. IEEE transactions on pattern analysis and machine intelligence, 1996, 18(6): 607-616.

[15] Friedman J H. Flexible metric nearest neighbor classification[R]. Technical report, Department of Statistics, Stanford University, 1994.

[16] Hastie T, Tibshirani R. Discriminant adaptive nearest neighbor classification[J]. IEEE transactions on pattern analysis and machine intelligence, 1996, 18(6): 607-616.

[17] Cover T, Hart P. Nearest neighbor pattern classification[J]. IEEE transactions on information theory, 1967, 13(1): 21-27.