KNN K-Nearest Neighbor Learning and Implementation in Python

• Take a simple example to explain this algorithm:
• How does the KNN algorithm work?
• Implementation in Python
• Example 2
• Explain some parameters in the functions
• When to use the KNN Algorithm
• How do we choose the factor K?

K Nearest Neighbor is one of classification algorithms that are very simple to understand but works incredibly well in practice. Also it is surprisingly versatile and its applications range from vision to proteins to computational geometry to graphs and so on.

When a prediction is required for a unseen data instance, the kNN algorithm will search through the training dataset for the k-most similar instances. The prediction attribute of the most similar instances is summarized and returned as the prediction for the unseen instance.

Take a simple example to explain this algorithm:

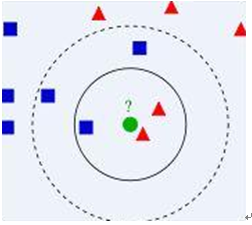
Look at the above image, we have two type data, including blue diamond and red triangle. Assume that we have the green data to determine it belong to which class. How do we do it? We think that only the nearest ones are helpful to find its classification. But how many to determine it? if we choose K=3, then there are 2 red triangles and 1 blue diamond, so we think green one is the same classification of the red one. If we choose K=5, then there are 2 red triangles and 3 blue diamond, so we think green one is the same classification of the blue one.

How does the KNN algorithm work?

Step 1: Calculate the distances between the current node and the nodes in the dataset

Step 2: Sort all the distances

Step 3: Calculate the frequency of the first K nodes in the classes

Step 4: Return the classification with the highest frequence

Implementation in Python

An example in scikit-learn pakage

import numpy as np
import matplotlib.pyplot as plt
from matplotlib.colors import ListedColormap
from sklearn import neighbors, datasets

# import data to play with
iris = datasets.load_iris()
# only two the first two features
X = iris.data[:, :2]
y = iris.target
h = 0.2 # step size in the mesh
n_neighbors = 15

# create the color maps
cmap_light = ListedColormap(['#FFAAAA', '#AAFFAA', '#AAAAFF'])
cmap_bold = ListedColormap(['#FF0000', '#00FF00', '#0000FF'])

for weights in ['uniform', 'distance']:
    # KNN
    clf = neighbors.KNeighborsClassifier(n_neighbors, weights=weights)
    clf.fit(X, y)

    # plot the decision boundary
    x_min, x_max = X[:, 0].min() - 1, X[:, 0].max() + 1
    y_min, y_max = X[:, 1].min() - 1, X[:, 1].max() + 1
    xx, yy = np.meshgrid(np.arange(x_min, x_max, h),
                         np.arange(y_min, y_max, h))
    Z = clf.predict(np.c_[xx.ravel(), yy.ravel()])
    Z = Z.reshape(xx.shape)
    plt.figure()
    plt.pcolormesh(xx, yy, Z, cmap = cmap_light)
    plt.scatter(X[:, 0], X[:, 1], c=y, cmap=cmap_bold)
    plt.xlim(xx.min(), xx.max())
    plt.ylim(yy.min(), yy.max())
    plt.title("3-Class classification (k = %i, weights = '%s')"
              % (n_neighbors, weights))

plt.show()

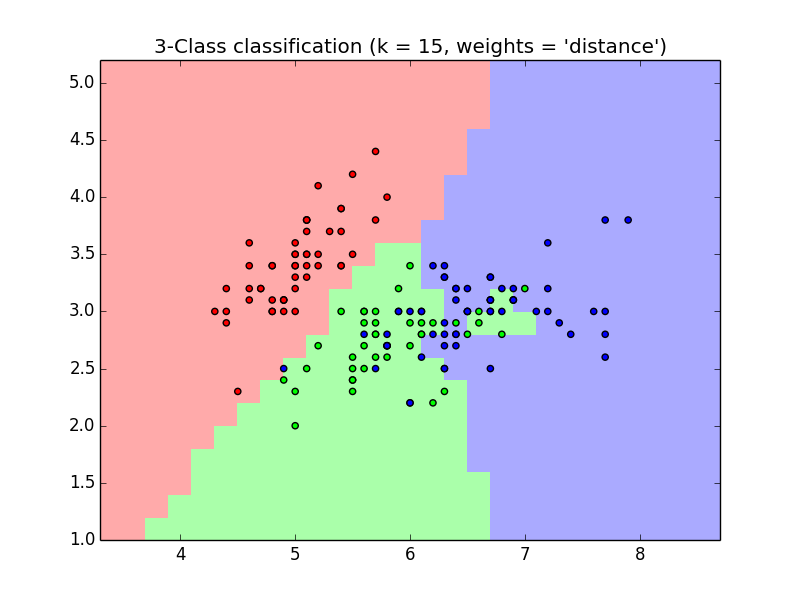
Example 2

import numpy as np
from sklearn import neighbors

knn = neighbors.KNeighborsClassifier()
data = np.array([[3,104],[2,100],[1,81],[101,10],[99,5],[98,2]])
labels = np.array([1,1,1,2,2,2])
knn.fit(data, labels)
knn.predict([18,90])

Explain some parameters in the functions

class sklearn.neighbors.KNeighborsClassifier(n_neighbors=5, weights=’uniform’, algorithm=’auto’, leaf_size=30, p=2, metric=’minkowski’, metric_params=None, n_jobs=1, **kwargs)[source].

n_neighbors: k, means the number of neighbors, default = 5.

weights : str or callable, optional (default = ‘uniform’). ‘uniform’ means all points in each neighborhood are weighted equally. ‘distance’ means that weight points by the inverse of their distance. [callable] : a user-defined function which accepts an array of distances, and returns an array of the same shape containing the weights.

algorithm: ‘auto’, ‘ball_tree’, ‘kd_tree’, ‘brute’.

leaf_size: Leaf size passed to BallTree or KDTree. This can affect the speed of the construction and query, as well as the memory required to store the tree. The optimal value depends on the nature of the problem.

metric: the distance metric to use for the tree.

p: Power parameter for the Minkowski metric.

metric_params: Additional keyword arguments for the metric function.

n_jobs: The number of parallel jobs to run for neighbors search.

When to use the KNN Algorithm

KNN can be used for both classification and regression predictive problems. There are 3 import aspects:

1. Ease to interpret output

2. Calculation time

3. Predictive Power. Graph based KNN is used in protein interaction prediction.

How do we choose the factor K?

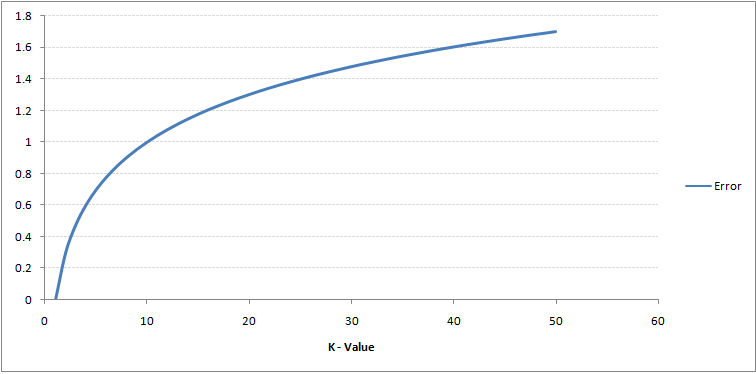
As you can see, the error rate at K=1 is always zero for the training sample. This is because the closest point to any training data point is itself.Hence the prediction is always accurate with K=1. If validation error curve would have been similar, our choice of K would have been 1. Following is the validation error curve with varying value of K:

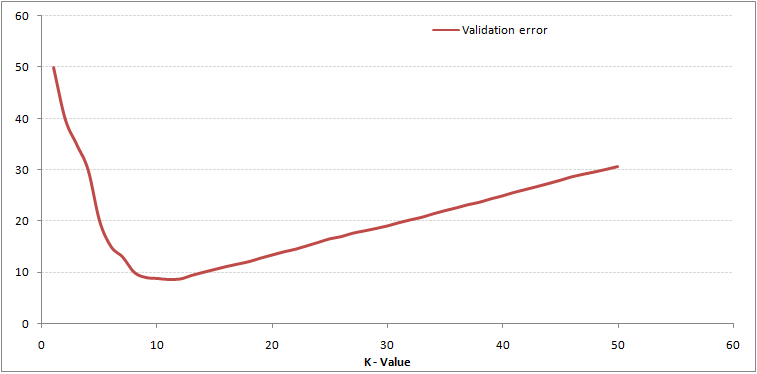
This makes the story more clear. At K=1, we were overfitting the boundaries. Hence, error rate initially decreases and reaches a minima. After the minima point, it then increase with increasing K. To get the optimal value of K, you can segregate the training and validation from the initial dataset. Now plot the validation error curve to get the optimal value of K. This value of K should be used for all predictions.